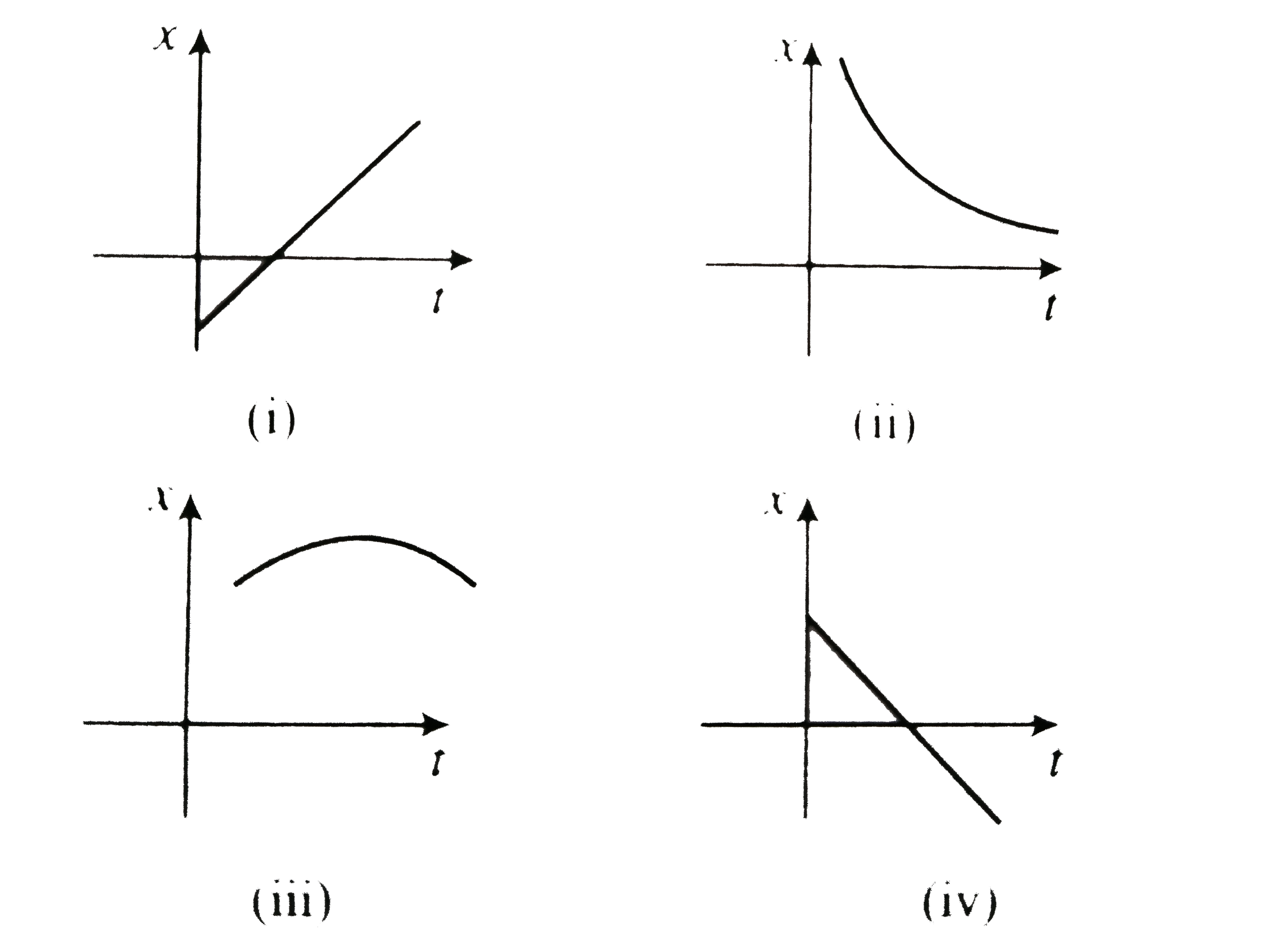
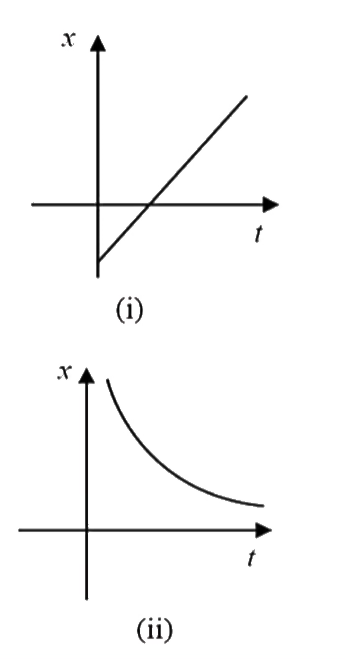
Study the following graph:
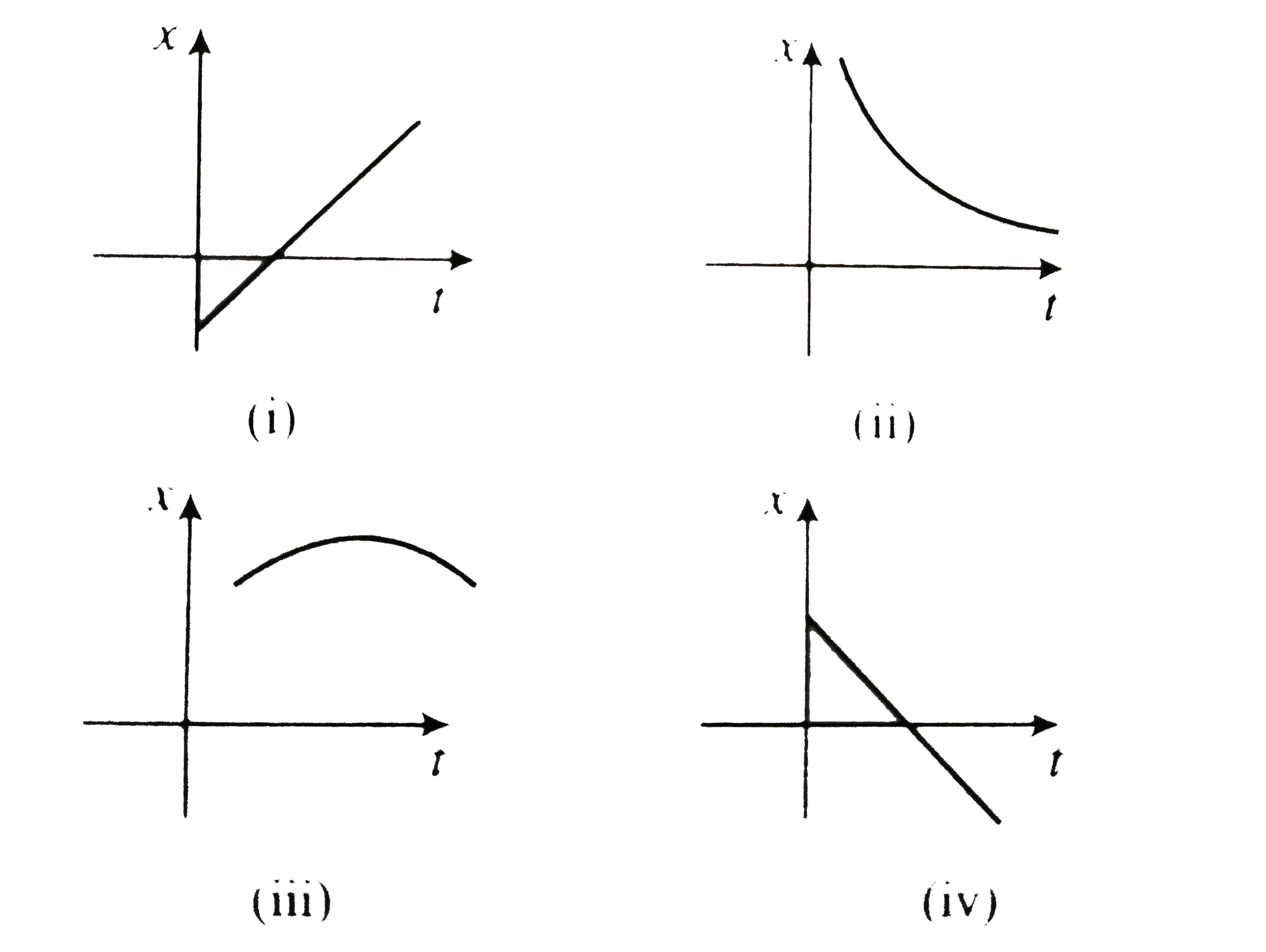
The particle is moving with constant speed .
In graph (i) and (iii)
In graph (i) and (iv)
In graph (i) and (ii)
In graph (i)
The correct Answer is:b
d. For the graph (i) aand (iv), slope is constant, hence the velocity is constant.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Assertion-reasoning
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
Knowledge Check
the circular motion of a particle with constant speed is
Aperiodic and simple harmonicBsimple harmonic but not periodicCneither periodic nor simple harmonicDperiodic but not simple harmonicWhich of the following graphs represents the position time-graph of a particle moving with negative velocity?
A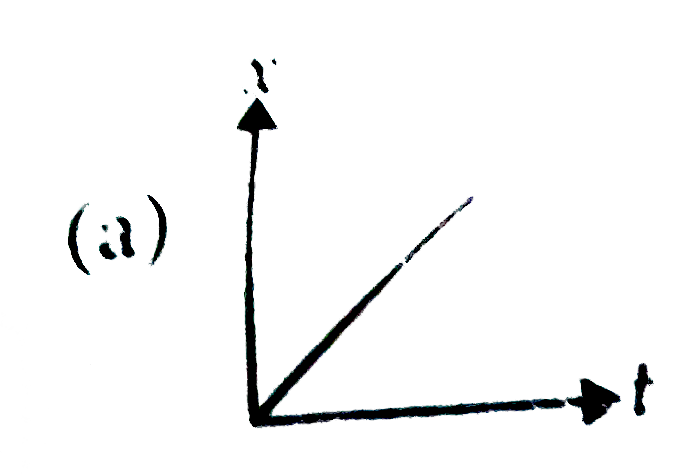 B
B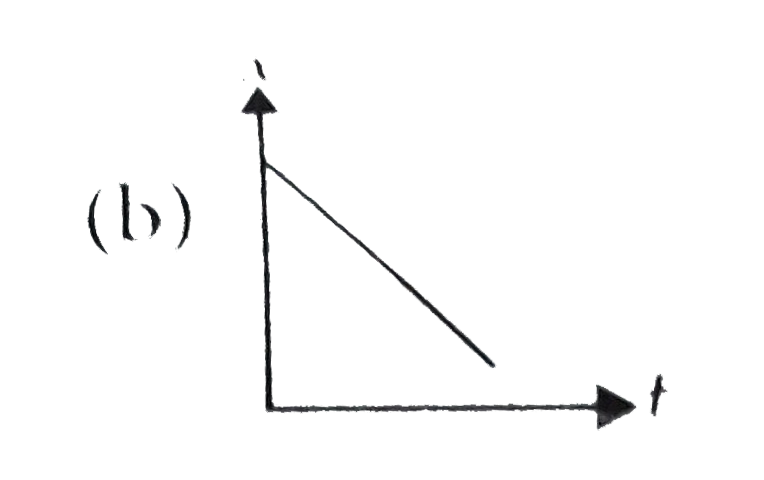 C
C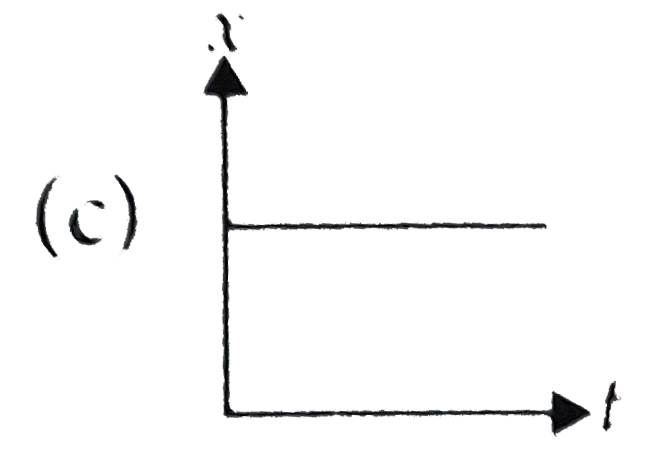 D
D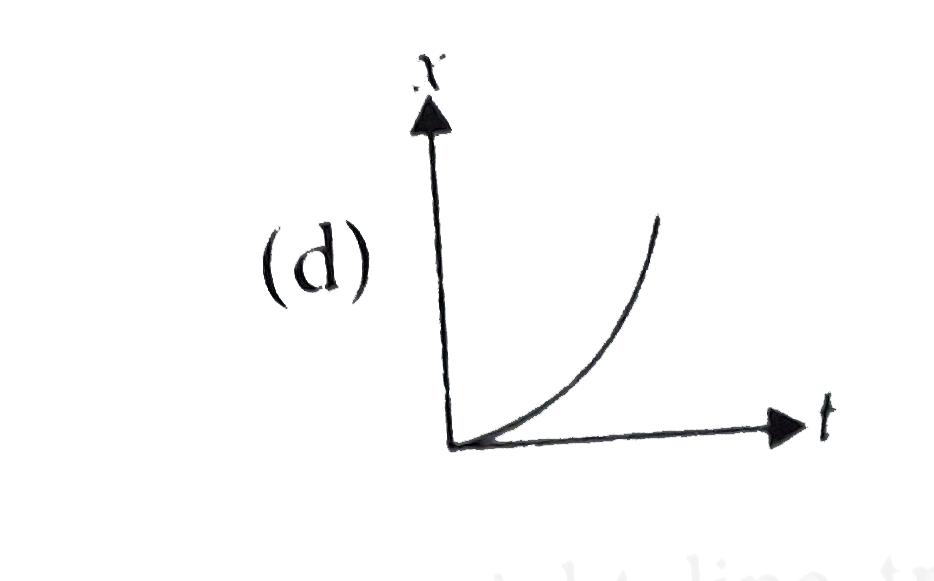
In the diagram shown, a particle is moving from the point A to the point B. Length of each arrow is 1 m and the particle is moving at a constant speed of 1ms−1 . What is the displacement of the particle?
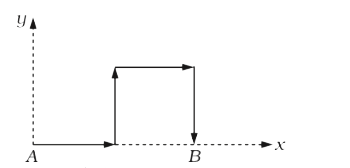
View SolutionStudy the following graph and mark the incorrect statement following it .

View SolutionWhen a particle moves in a circle with a uniform speed
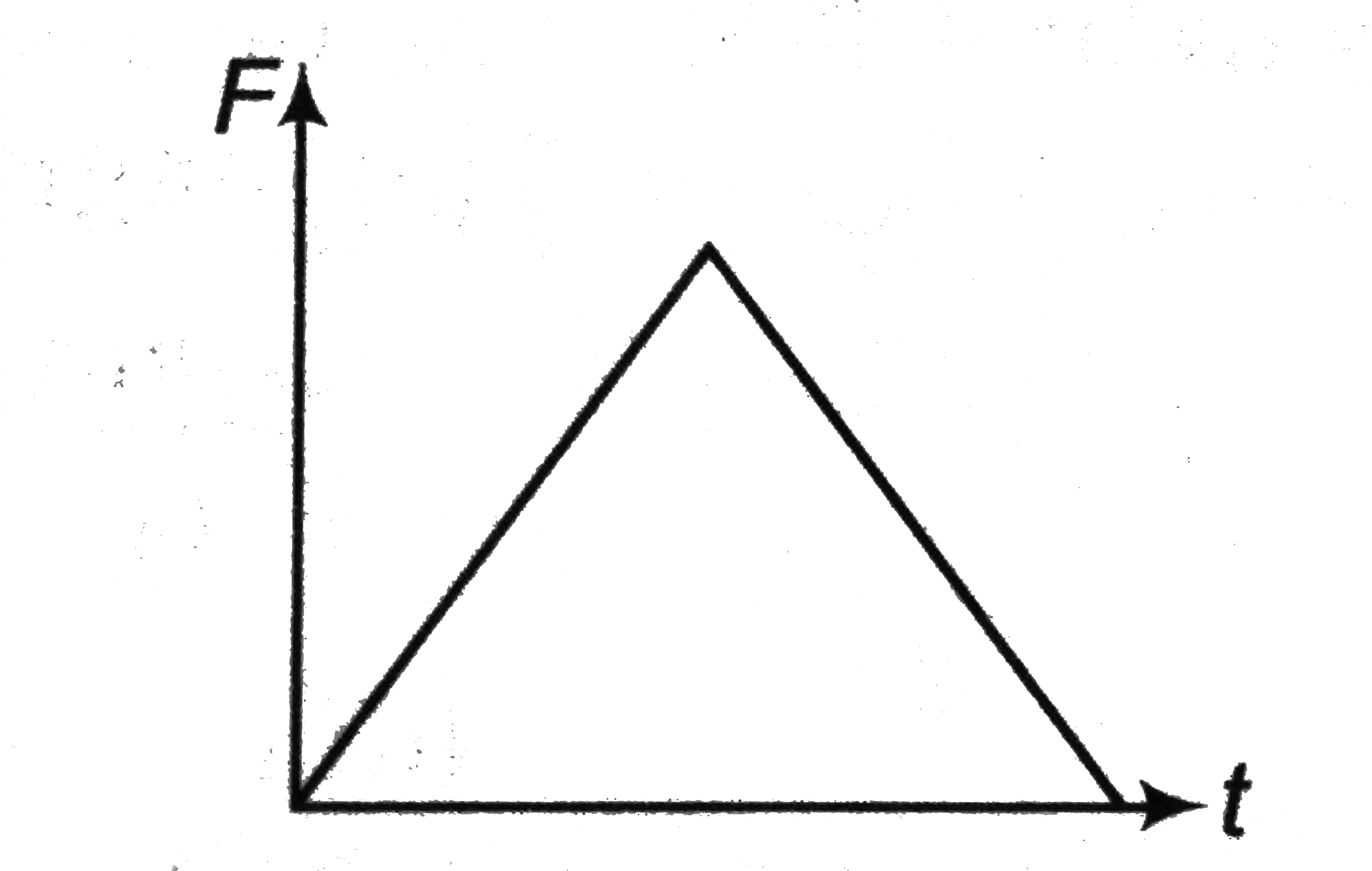
View SolutionThe net force acting on a particle moving along a straight line varies with time as shown in the diagram. Force is parallel to velocity. Which of the following graph is best representative of its speed with time? (Initial velocity of the particle is zero)
View SolutionIt has been postulated that there may be some particle moving with speed greater than the speed of light. Such particles have been named as
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View Solution