A parachutist after bailing out falls 50m without friction. When parachute opens, it decelerates at 2m/s2. He reaches the ground with a speed of 3m/s. At what height, did the bail out?
To solve the problem step by step, we will break down the process of finding the height from which the parachutist bailed out.
Step 1: Calculate the velocity after falling 50 meters
The parachutist falls freely for 50 meters. We can use the equation of motion to find the velocity after falling this distance. The equation we will use is:
v2=u2+2gh
Where:
- v = final velocity after falling 50 m
- u = initial velocity (0 m/s, since he starts from rest)
- g = acceleration due to gravity (approximately 10 m/s²)
- h = height fallen (50 m)
Substituting the values:
v2=0+2⋅10⋅50
v2=1000
v=√1000
v=31.62m/s
Step 2: Use the deceleration to find the distance fallen after the parachute opens
After the parachute opens, the parachutist decelerates at a=−2m/s2 until he reaches the ground with a final velocity of v=3m/s. We can use the same equation of motion:
v2=u2+2as
Where:
- v=3m/s (final velocity)
- u=31.62m/s (initial velocity after falling 50 m)
- a=−2m/s2 (deceleration)
- s = distance fallen after the parachute opens
Substituting the values:
32=(31.62)2+2⋅(−2)⋅s
9=1000−4s
4s=1000−9
4s=991
s=9914
s=247.75m
Step 3: Calculate the total height from which the parachutist bailed out
The total height H from which the parachutist bailed out is the sum of the height fallen freely (50 m) and the distance fallen after the parachute opened (247.75 m):
H=50+247.75
H=297.75m
Final Answer
The total height from which the parachutist bailed out is approximately 298 meters.
---
The parachutist falls freely for 50 meters. We can use the equation of motion to find the velocity after falling this distance. The equation we will use is:
- v = final velocity after falling 50 m
- u = initial velocity (0 m/s, since he starts from rest)
- g = acceleration due to gravity (approximately 10 m/s²)
- h = height fallen (50 m)
v2=1000
v=√1000
v=31.62m/s
After the parachute opens, the parachutist decelerates at a=−2m/s2 until he reaches the ground with a final velocity of v=3m/s. We can use the same equation of motion:
- v=3m/s (final velocity)
- u=31.62m/s (initial velocity after falling 50 m)
- a=−2m/s2 (deceleration)
- s = distance fallen after the parachute opens
9=1000−4s
4s=1000−9
4s=991
s=9914
s=247.75m
The total height H from which the parachutist bailed out is the sum of the height fallen freely (50 m) and the distance fallen after the parachute opened (247.75 m):
H=297.75m
The total height from which the parachutist bailed out is approximately 298 meters.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.315videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.416videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.117videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
A parachutist after bailing out falls 52 m without friction. When the parachute opens, she decelerates at 2.1ms−2 & reaches the ground with a speed of 2.9ms−1.
(i) How long has been the parachutist in the air? (ii) At what height did the fall begin?View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View SolutionA ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
View SolutionA parachutist drops freely from an aeroplane for 10 seconds before the parachute opens out.Then he descends with a net retardation of 2m/sec2.
His velocity whe he reaches the ground is 8m/sec.Find the height at which he get out of the aeroplane?View SolutionA parachutist drops freely from helicopter for 20 s before the parachute opends out. Then he descends with retardation of 40ms2. The height of the helicopter from the ground level is 2500m. When he drops out, his velocity on reaching the ground will be
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
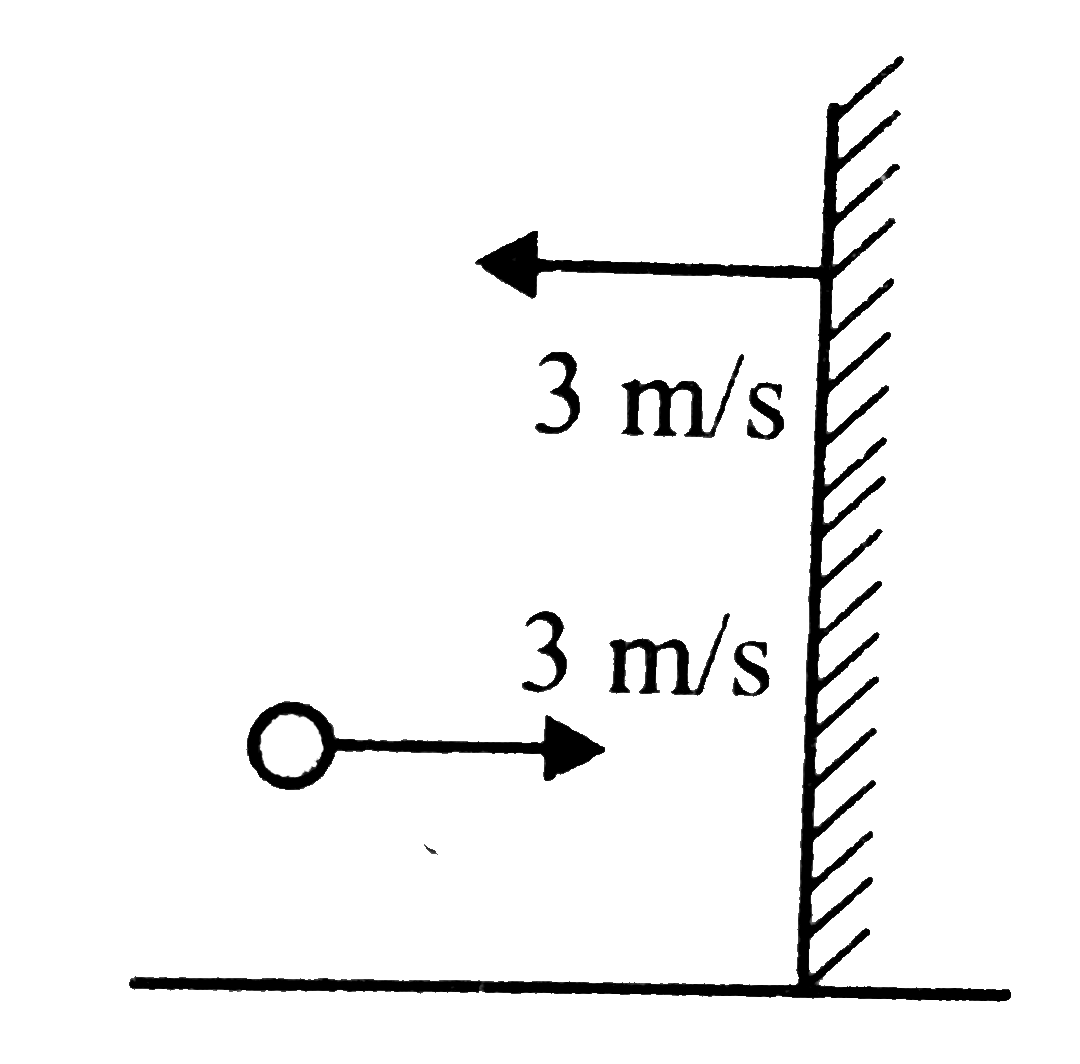 View Solution
View SolutionA parachutist drops first freely form an areophone for 10s and then his parachut opens out. Now he descends with a net retardtion of 2.5ms−2 If the balil out of the plane at a height of 2495m and g=10ms−2, his velocity on reaching the ground will be.
View SolutionA shell of mass 4kg moving with a velocoity 10m/s vertically upward explodes into three parts at a height 50m from ground. After three seconds, one part of mass 2kg reaches ground and another part of mass 1kg is at height 40m from ground. The height of the third part from the ground is : [g=10m/s2]
View SolutionA shell of mass 4kg moving with a velocoity 10m/s vertically upward explodes into three parts at a height 50m from ground. After three seconds, one part of mass 2kg reaches ground and another part of mass 1kg is at height 40m from ground. The height of the third part from the ground is : [g=10m/s2]
View SolutionA particle of mass 2m is dropped from a height 80 m above the ground. At the same time another particle of mass m is thrown vertically upwards from the ground with a speed of 40 m/s. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of second is:
View Solution
