A bouy is attached to three tugboats by three ropes. The tugboats are engaged in a tug-0f-war. One tugboat pulls west on the buoy with a force →F1 of magnitude 1000N. The second tugboat pulls south on the buoy with a force →F2 of magnitude 2000N. The third tugboat pulls northeast (that is, half way between north and east), with a force →F3 of magnitude 2000N
a. Express each force in unit vector from (ˆi,ˆj).
b. Calculate the magnitude of the resultant force.
The correct Answer is:a.x=→Fx=1000(√2−1ˆi; b. y= -1000(2-sqrt(2)) hat(j)
To solve the problem step by step, we will break it down into two parts as per the question.
Part (a): Express each force in unit vector form
1. Identify the forces and their directions:
- Tugboat 1 pulls west with a force F1=1000N.
- Tugboat 2 pulls south with a force F2=2000N.
- Tugboat 3 pulls northeast with a force F3=2000N.
2. Convert each force into unit vector form:
- For F1 (west):
→F1=−1000^iN
- For F2 (south):
→F2=−2000^jN
- For F3 (northeast):
- The angle for northeast is 45∘.
- The components can be calculated using:
→F3=2000cos(45∘)^i+2000sin(45∘)^j
Since cos(45∘)=sin(45∘)=1√2:
→F3=2000(1√2)^i+2000(1√2)^j=1000√2^i+1000√2^j
3. Final expressions for each force:
→F1=−1000^iN
→F2=−2000^jN
→F3=1000√2^i+1000√2^jN
Part (b): Calculate the magnitude of the resultant force
1. Sum the forces:
→Fnet=→F1+→F2+→F3
Substituting the expressions:
→Fnet=(−1000^i)+(−2000^j)+(1000√2^i+1000√2^j)
2. Combine the ^i and ^j components:
- For ^i:
Fnet,i=−1000+1000√2
- For ^j:
Fnet,j=−2000+1000√2
3. Resultant force vector:
→Fnet=(−1000+1000√2)^i+(−2000+1000√2)^j
4. Calculate the magnitude of the resultant force:
|→Fnet|=√(Fnet,i)2+(Fnet,j)2
Substituting the values:
|→Fnet|=√(−1000+1000√2)2+(−2000+1000√2)2
5. Simplifying the expression:
- Calculate (−1000+1000√2)2 and (−2000+1000√2)2 separately, then add them and take the square root.
- Tugboat 1 pulls west with a force F1=1000N.
- Tugboat 2 pulls south with a force F2=2000N.
- Tugboat 3 pulls northeast with a force F3=2000N.
- For F1 (west):
→F1=−1000^iN
- For F2 (south):
→F2=−2000^jN
- For F3 (northeast):
- The angle for northeast is 45∘.
- The components can be calculated using:
→F3=2000cos(45∘)^i+2000sin(45∘)^j
Since cos(45∘)=sin(45∘)=1√2:
→F3=2000(1√2)^i+2000(1√2)^j=1000√2^i+1000√2^j
→F1=−1000^iN
→F2=−2000^jN
→F3=1000√2^i+1000√2^jN
→Fnet=→F1+→F2+→F3
Substituting the expressions:
→Fnet=(−1000^i)+(−2000^j)+(1000√2^i+1000√2^j)
- For ^i:
Fnet,i=−1000+1000√2
- For ^j:
Fnet,j=−2000+1000√2
→Fnet=(−1000+1000√2)^i+(−2000+1000√2)^j
|→Fnet|=√(Fnet,i)2+(Fnet,j)2
Substituting the values:
|→Fnet|=√(−1000+1000√2)2+(−2000+1000√2)2
- Calculate (−1000+1000√2)2 and (−2000+1000√2)2 separately, then add them and take the square root.
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Single Correct
Explore 51 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
In a tug of war competition, two men pull the ends of the rope with forces equal in magnitude and opposite in direction. What is the tension in the rope ?
View SolutionThe resultant of two forces has magnitude 20N. One of the forces is of magnitude 20√3N and makes an angle of 30∘ with the resultant. Then what is the magnitude of the other force?
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
Two forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionWhat is the angle between vectors →a and →b with magnitudes 2 and 3 respectively ? Given →a.→b=√3 .
View SolutionTwo forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
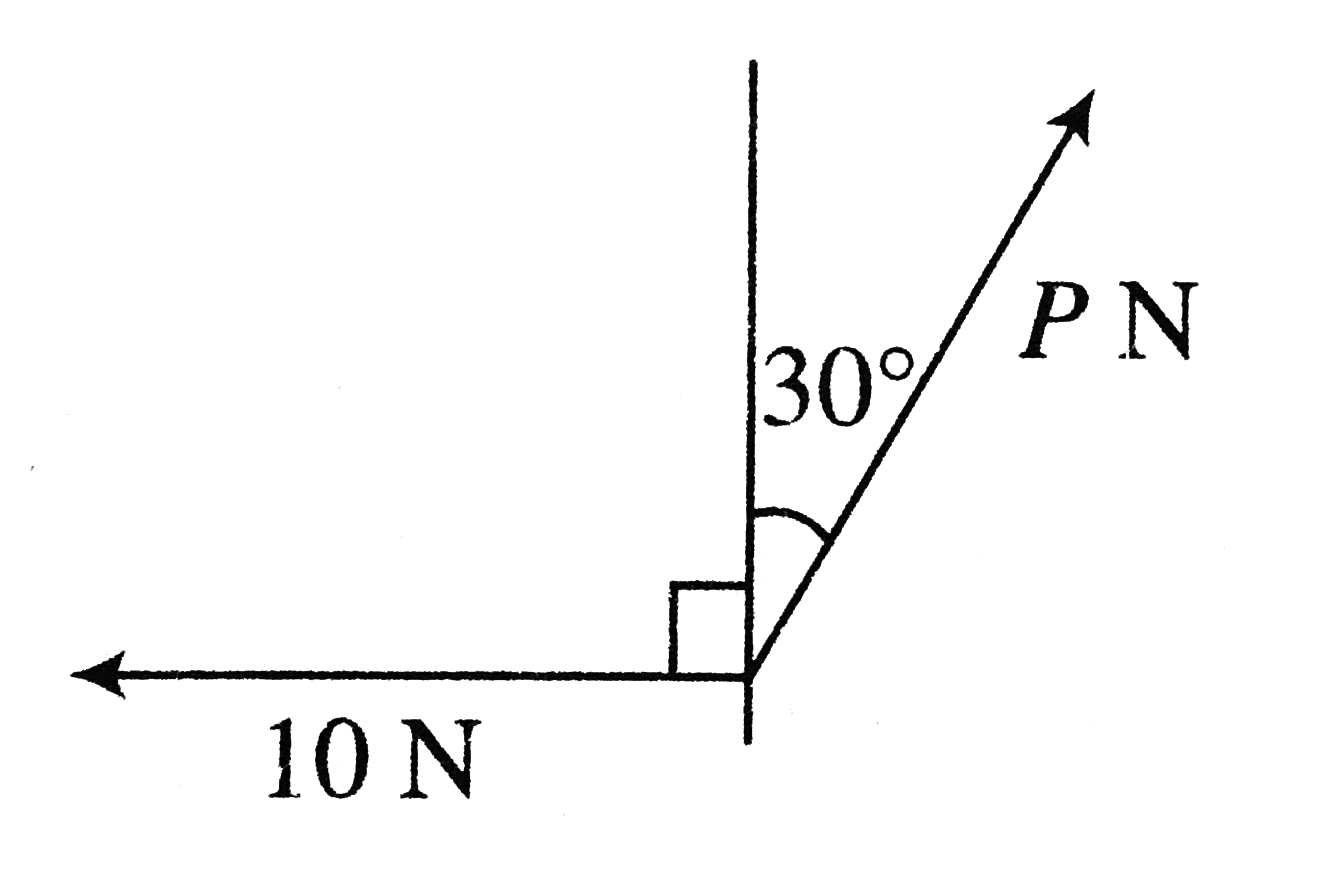
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionA block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
View SolutionIf two forces each of magnitude 20N, are acting on a particle such that the first force (→E1) is acting along east direction and the second force (vercF2) is acting along the direction 60∘ north of west, then the magnitude of resultant force on particle is
View Solution