The dimensions of intensity of wave are
The correct Answer is:B
To find the dimensions of intensity of a wave, we can follow these steps:
Step 1: Understand the Definition of Intensity
Intensity (I) is defined as power (P) per unit area (A). Mathematically, it can be expressed as:
I=PA
Step 2: Determine the Dimensions of Power
Power is defined as the rate of doing work or the rate of energy transfer. The dimensions of energy (E) are given by:
(E)=(M)(L2)(T−2)
where:
- M is mass,
- L is length,
- T is time.
Since power is energy per unit time, we have:
(P)=(E)(T)=(M)(L2)(T−2)(T)=(M)(L2)(T−3)
Step 3: Determine the Dimensions of Area
Area (A) is given by the square of length:
(A)=(L2)
Step 4: Combine Dimensions to Find Intensity
Substituting the dimensions of power and area into the intensity formula:
(I)=(P)(A)=(M)(L2)(T−3)(L2)
Step 5: Simplify the Expression
When we simplify the expression:
(I)=(M)(L2)(T−3)⋅(L−2)=(M)(L0)(T−3)=(M)(T−3)
Conclusion
Thus, the dimensions of intensity of a wave are:
(I)=(M)(T−3)
Final Answer
The dimensions of intensity of wave are (M)(T−3).
---
Intensity (I) is defined as power (P) per unit area (A). Mathematically, it can be expressed as:
I=PA
Power is defined as the rate of doing work or the rate of energy transfer. The dimensions of energy (E) are given by:
(E)=(M)(L2)(T−2)
where:
- M is mass,
- L is length,
- T is time.
(P)=(E)(T)=(M)(L2)(T−2)(T)=(M)(L2)(T−3)
Area (A) is given by the square of length:
(A)=(L2)
Substituting the dimensions of power and area into the intensity formula:
(I)=(P)(A)=(M)(L2)(T−3)(L2)
When we simplify the expression:
(I)=(M)(L2)(T−3)⋅(L−2)=(M)(L0)(T−3)=(M)(T−3)
Thus, the dimensions of intensity of a wave are:
(I)=(M)(T−3)
The dimensions of intensity of wave are (M)(T−3).
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct
2 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Linked Comprehension
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Subjective
31 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
The ratio of intensities of two waves are given by 4:1. The ratio of the amplitudes of the two waves is
View SolutionCalculate the ratio of intensity of wave train A to wave train B.
_E01_106_Q01.png)
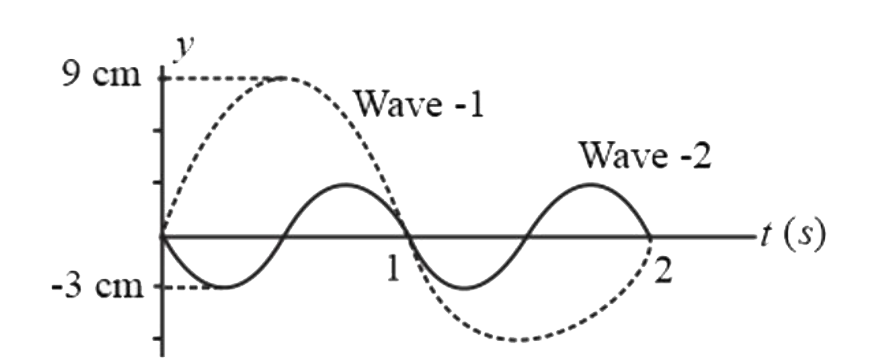
View SolutionDisplacement - time graphs for two waves, wave - 1 and wave - 2 are shown here. The ratio of the intensity of wave-1 to that of wave - 2 is
View SolutionTwo coherent sources produce waves of different intensities which interfere. A fter interference, the ratio of the maximum intensity to the minimum intensity is 16. The intensity of the waves are in the ratio :
View Solution(a) Explain the terms energy density and intensity of wave.
(b) Show that the intensity of a wave is proportional to the square of the amplitude.
View SolutionThe ratio of intensities of two waves is 2. the ratio of intensities of maxima and minima when these waves interfere is approximately
View SolutionThe ratio of intensities of two waves is 9:16. If these two waves interfere, then determine the ration of the maximum and minimum possible intensities.
View SolutionThe ratio of intensities of two waves is 16:9. What is the ratio of amplitudes? If these two waves produce interference, then find the ratio of maximum and minimum intensities.
View SolutionThe ratio of intensities of two waves is 9:1 When they superimpose, the ratio of maximum to minimum intensity will become :-
View SolutionThe ratio of intensities of two waves is 9:1 When they superimpose, the ratio of maximum to minimum intensity will become :-
View Solution
