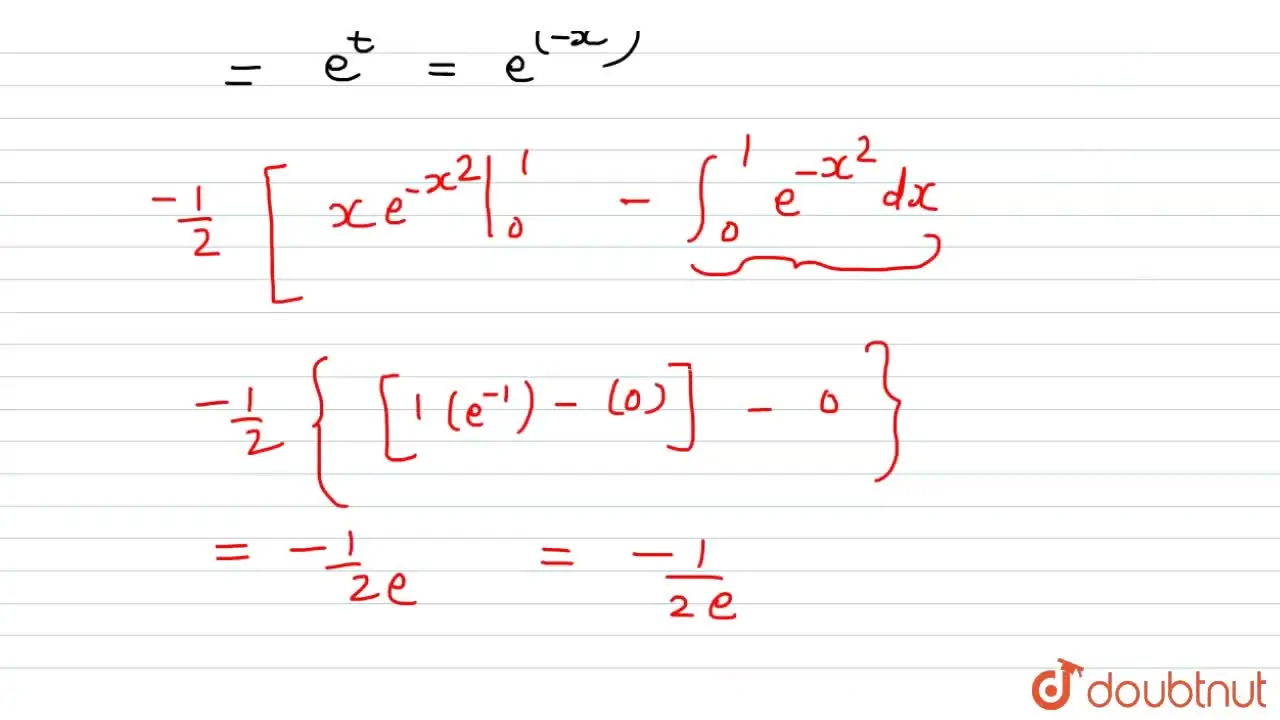If ∫10e−x2dx=0, then ∫10x2e−x2 dx is equal to
A
-(1)/(2e)
B
12e(e+1)
C
1e(e−1)
D
1e(e+1)
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video & image solution for If int _(0)^(1) e ^(-x ^(2)) dx =0, then int _(0)^(1) x ^(2)e ^(-x ^(2)) dx is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - VK JAISWAL ENGLISHCHAPTER - INDEFINITE AND DEFINITE INTEGRATIONEXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)15videos
INDEFINITE AND DEFINITE INTEGRATION
- BOOK - VK JAISWAL ENGLISHCHAPTER - INDEFINITE AND DEFINITE INTEGRATIONEXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)16videos
INDEFINITE AND DEFINITE INTEGRATION
- BOOK - VK JAISWAL ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise-4 : Subjective Type Problems3videos
HYPERBOLA
- BOOK - VK JAISWAL ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNTIONS EXERCISE - Exercise-5 : Subjective Type Problems6videos
INVERSE TRIGONOMETRIC FUNTIONS
Similar Questions
If ∫10e−x2dx=a, then ∫10x2e−x2 dx is equal to
View Solution∫10xex2dx
View Solution∫20exdx
View SolutionIf ∫10ex1+xdx=k, then ∫10ex(1+x)2dx is equal to
View Solution∫10dxex+e−x is equal to
View Solution∫10dxex+e−x is equal to
View SolutionIf I=∫10(1+e−x2)dx then, s
View Solution∫20ex dx
View Solution∫10xexdx=1
View Solution∫10e2xeex dx =)
View Solution