Which of the following compound has the smallest bond angle (X-A-X) in each series respectively ?
(A) OSF2 OSCl2 OSBr2
(B)SbCl3 SbBr3 SbI3
(C )PI3 AsI3 SbI3
OSF2,SbCl3andPI3
OSBr2,SbI3andPI3
OSF2,SbI3andPI3
OSF2,SbCl3andSbI3
The correct Answer is:D
To determine which compound has the smallest bond angle (X-A-X) in each series, we will analyze each series based on the electronegativity of the atoms involved and the resulting crowding effects.
1. Identify the central atom: In all three compounds, sulfur (S) is the central atom.
2. Consider the electronegativity of the halogens:
- Fluorine (F) is the most electronegative, followed by chlorine (Cl), and then bromine (Br).
3. Analyze the effect of electronegativity on bond angles:
- The more electronegative the halogen, the more it pulls the bonding electrons towards itself, reducing electron repulsion around the central atom.
- OSF₂ will have the least crowding around sulfur due to the high electronegativity of fluorine, leading to the smallest bond angle.
4. Conclusion for Series A: The compound with the smallest bond angle is OSF₂.
Series B: SbCl₃, SbBr₃, SbI₃
1. Identify the central atom: In all three compounds, antimony (Sb) is the central atom.
2. Consider the electronegativity of the halogens:
- Chlorine (Cl) is the most electronegative, followed by bromine (Br), and then iodine (I).
3. Analyze the effect of electronegativity on bond angles:
- Similar to Series A, the more electronegative the halogen, the less crowding around the central atom.
- SbCl₃ will have the least crowding due to chlorine's high electronegativity, resulting in the smallest bond angle.
4. Conclusion for Series B: The compound with the smallest bond angle is SbCl₃.
Series C: PI₃, AsI₃, SbI₃
1. Identify the central atom: The central atoms are phosphorus (P), arsenic (As), and antimony (Sb) respectively.
2. Consider the electronegativity of the central atoms:
- Phosphorus is the most electronegative, followed by arsenic, and then antimony.
3. Analyze the effect of electronegativity on bond angles:
- As we move down the group, the electronegativity decreases, leading to increased crowding around the central atom.
- PI₃ will have the most crowding due to phosphorus's high electronegativity, resulting in a larger bond angle.
- Conversely, SbI₃ will have the least crowding and thus the smallest bond angle.
4. Conclusion for Series C: The compound with the smallest bond angle is SbI₃.
Final Answers:
- Series A: OSF₂
- Series B: SbCl₃
- Series C: SbI₃
Overall Conclusion:
The compounds with the smallest bond angles in each series are:
1. OSF₂
2. SbCl₃
3. SbI₃
2. Consider the electronegativity of the halogens:
- Fluorine (F) is the most electronegative, followed by chlorine (Cl), and then bromine (Br).
3. Analyze the effect of electronegativity on bond angles:
- The more electronegative the halogen, the more it pulls the bonding electrons towards itself, reducing electron repulsion around the central atom.
- OSF₂ will have the least crowding around sulfur due to the high electronegativity of fluorine, leading to the smallest bond angle.
4. Conclusion for Series A: The compound with the smallest bond angle is OSF₂.
2. Consider the electronegativity of the halogens:
- Chlorine (Cl) is the most electronegative, followed by bromine (Br), and then iodine (I).
3. Analyze the effect of electronegativity on bond angles:
- Similar to Series A, the more electronegative the halogen, the less crowding around the central atom.
- SbCl₃ will have the least crowding due to chlorine's high electronegativity, resulting in the smallest bond angle.
4. Conclusion for Series B: The compound with the smallest bond angle is SbCl₃.
2. Consider the electronegativity of the central atoms:
- Phosphorus is the most electronegative, followed by arsenic, and then antimony.
3. Analyze the effect of electronegativity on bond angles:
- As we move down the group, the electronegativity decreases, leading to increased crowding around the central atom.
- PI₃ will have the most crowding due to phosphorus's high electronegativity, resulting in a larger bond angle.
- Conversely, SbI₃ will have the least crowding and thus the smallest bond angle.
4. Conclusion for Series C: The compound with the smallest bond angle is SbI₃.
- Series A: OSF₂
- Series B: SbCl₃
- Series C: SbI₃
The compounds with the smallest bond angles in each series are:
1. OSF₂
2. SbCl₃
3. SbI₃
Topper's Solved these Questions
- CHEMICAL BONDING (BASIC)Book:VK JAISWAL ENGLISHChapter:CHEMICAL BONDING (BASIC)Exercise:Level 3 (Passive 1)
Explore 6 Videos
- CHEMICAL BONDING (BASIC)Book:VK JAISWAL ENGLISHChapter:CHEMICAL BONDING (BASIC)Exercise:Level 3 (Passive 2)
Explore 6 Videos
- CHEMICAL BONDING (BASIC)Book:VK JAISWAL ENGLISHChapter:CHEMICAL BONDING (BASIC)Exercise:SUBJECTIVE PROBLEMS
Explore 54 Videos
- CHEMICAL BONDING (ADVANCED)Book:VK JAISWAL ENGLISHChapter:CHEMICAL BONDING (ADVANCED)Exercise:SUBJECTIVE PROBLEMS
Explore 64 Videos
- CO-ORDINATION COMPOUNDSBook:VK JAISWAL ENGLISHChapter:CO-ORDINATION COMPOUNDSExercise:LEVEL 2
Explore 144 Videos
Similar Questions
Which of the following compound has the smallest (X−A−X) bond angle in each series repectively.
(A) OsF2,OsCl2,OsBr2
(B) SbCl3,SbBr3,SbI3
(C) Pl3,AsI3,SbI3
View SolutionWhich of the following has larger bond angle in the following pairs ?
(a)NH3,PH3(b)BeF2,BF3(c)H2O,CO2(d)H2O,H2S(e)CCL4,C2H2 ?
View SolutionIn the compound ,
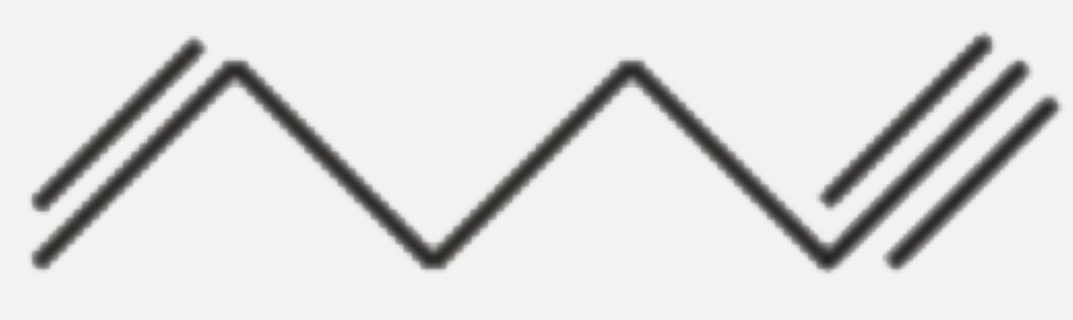 , the C2 - C3 bond is of the type :
, the C2 - C3 bond is of the type :
View SolutionThe smallest of values of x2−3x+3 in the interval [−3,32] is a. -20 b. -15 c. 5 d. 3/4
View SolutionWhich of the following equations has the sum of its roots as 3? (a) x2+3x−5=0 (b) −x2+3x+3=0 (c) √2x2−3√2x−1=0 (d) 3x2−3x−3=0
View SolutionWhich of the following equations has the sum of its roots as 3?
(a)x2+3x−5=0
(b) −x2+3x+3=0
(c)√2x2−3√2x−1=0
(d) 3x2−3x−3=0
View SolutionIs the following statements are correct ?
(i)Among NH3,PH3,AsH3,andSbH3,SbH3 has smallest bond angle.
(ii)Among SbCl3,SbBr3,andSbl3,Sbl3 has the largest bond angle.
View SolutionDifferentiate each of the following with respect to x in following question: (2x−7)2(3x+5)3
View SolutionWhich of the following is not the root of the equation ∣∣ ∣∣x−6−12−3xx−3−32xx+2∣∣ ∣∣=0? a.2 b. 0 c. 1 d. −3
View SolutionThe value of a for which the function f(x)=asinx+(13)sin3x has an extremum at x=π3 is (a) 1 (b) −1 (c) 0 (d) 2
View Solution