Incorrect order of solubility product (Ksp) of given precipitated compound is:
AgCl<PbCl2
Al(OH)3<Zn(OH)2
BaCO3<MgCO3
MnS<Ag2S
The correct Answer is:D
To determine the incorrect order of solubility products (Ksp) for the given precipitated compounds, we will analyze each pair of compounds step by step.
Step 1: Analyze AgCl and PbCl2
- Dissociation:
- AgCl dissociates into Ag⁺ and Cl⁻:
AgCl⇌Ag++Cl−
- Let the solubility of AgCl be S. Therefore, Ksp=S2.
- PbCl2 dissociates into Pb²⁺ and 2Cl⁻:
PbCl2⇌Pb2++2Cl−
- Let the solubility of PbCl2 be S′. Therefore, Ksp=(Pb2+)(Cl−)2=S′⋅(2S′)2=4S′3.
- Comparison:
- Since Ksp for PbCl2 is greater than that for AgCl, this order is correct:
Ksp(PbCl2)>Ksp(AgCl)
Step 2: Analyze Al(OH)3 and Zn(OH)2
- Dissociation:
- Al(OH)3 dissociates into Al³⁺ and 3OH⁻:
Al(OH)3⇌Al3++3OH−
- Let the solubility of Al(OH)3 be S. Therefore, Ksp=S⋅(3S)3=27S4.
- Zn(OH)2 dissociates into Zn²⁺ and 2OH⁻:
Zn(OH)2⇌Zn2++2OH−
- Let the solubility of Zn(OH)2 be S′. Therefore, Ksp=S′⋅(2S′)2=4S′3.
- Comparison:
- Al(OH)3 precipitates first due to lower OH⁻ concentration, thus having a lower Ksp:
Ksp(Al(OH)3)<Ksp(Zn(OH)2)
- This order is correct.
Step 3: Analyze BaCO3 and MgCO3
- Dissociation:
- BaCO3 dissociates into Ba²⁺ and CO3²⁻:
BaCO3⇌Ba2++CO2−3
- MgCO3 dissociates into Mg²⁺ and CO3²⁻:
MgCO3⇌Mg2++CO2−3
- Comparison:
- As we move down the group in the periodic table, the solubility decreases. Therefore, MgCO3 has a higher solubility than BaCO3:
Ksp(MgCO3)>Ksp(BaCO3)
- This order is correct.
Step 4: Analyze Ag2S and MnS
- Dissociation:
- Ag2S dissociates into 2Ag⁺ and S²⁻:
Ag2S⇌2Ag++S2−
- Let the solubility of Ag2S be S. Therefore, Ksp=(2S)2⋅S=4S3.
- MnS dissociates into Mn²⁺ and S²⁻:
MnS⇌Mn2++S2−
- Let the solubility of MnS be S′. Therefore, Ksp=S′⋅S′=S′2.
- Comparison:
- Ag2S precipitates first (lower Ksp) compared to MnS:
Ksp(Ag2S)<Ksp(MnS)
- The order given (Ksp of Ag2S > Ksp of MnS) is incorrect.
Conclusion
The incorrect order of solubility products (Ksp) is:
Ksp(Ag2S)>Ksp(MnS)
Final Answer
The correct answer is option 4.
---
- Dissociation:
- AgCl dissociates into Ag⁺ and Cl⁻:
AgCl⇌Ag++Cl−
- Let the solubility of AgCl be S. Therefore, Ksp=S2.
- PbCl2 dissociates into Pb²⁺ and 2Cl⁻:
PbCl2⇌Pb2++2Cl−
- Let the solubility of PbCl2 be S′. Therefore, Ksp=(Pb2+)(Cl−)2=S′⋅(2S′)2=4S′3.
- Since Ksp for PbCl2 is greater than that for AgCl, this order is correct:
Ksp(PbCl2)>Ksp(AgCl)
- Dissociation:
- Al(OH)3 dissociates into Al³⁺ and 3OH⁻:
Al(OH)3⇌Al3++3OH−
- Let the solubility of Al(OH)3 be S. Therefore, Ksp=S⋅(3S)3=27S4.
- Zn(OH)2 dissociates into Zn²⁺ and 2OH⁻:
Zn(OH)2⇌Zn2++2OH−
- Let the solubility of Zn(OH)2 be S′. Therefore, Ksp=S′⋅(2S′)2=4S′3.
- Al(OH)3 precipitates first due to lower OH⁻ concentration, thus having a lower Ksp:
Ksp(Al(OH)3)<Ksp(Zn(OH)2)
- This order is correct.
- Dissociation:
- BaCO3 dissociates into Ba²⁺ and CO3²⁻:
BaCO3⇌Ba2++CO2−3
- MgCO3 dissociates into Mg²⁺ and CO3²⁻:
MgCO3⇌Mg2++CO2−3
- As we move down the group in the periodic table, the solubility decreases. Therefore, MgCO3 has a higher solubility than BaCO3:
Ksp(MgCO3)>Ksp(BaCO3)
- This order is correct.
- Dissociation:
- Ag2S dissociates into 2Ag⁺ and S²⁻:
Ag2S⇌2Ag++S2−
- Let the solubility of Ag2S be S. Therefore, Ksp=(2S)2⋅S=4S3.
- MnS dissociates into Mn²⁺ and S²⁻:
MnS⇌Mn2++S2−
- Let the solubility of MnS be S′. Therefore, Ksp=S′⋅S′=S′2.
- Ag2S precipitates first (lower Ksp) compared to MnS:
Ksp(Ag2S)<Ksp(MnS)
- The order given (Ksp of Ag2S > Ksp of MnS) is incorrect.
The incorrect order of solubility products (Ksp) is:
Ksp(Ag2S)>Ksp(MnS)
The correct answer is option 4.
Topper's Solved these Questions
- QUALITATIVE INORGANIC ANALYSISBook:VK JAISWAL ENGLISHChapter:QUALITATIVE INORGANIC ANALYSISExercise:LEVEL 2
Explore 76 Videos
- QUALITATIVE INORGANIC ANALYSISBook:VK JAISWAL ENGLISHChapter:QUALITATIVE INORGANIC ANALYSISExercise:LEVEL 3
Explore 62 Videos
- PERIODIC PROPERTIESBook:VK JAISWAL ENGLISHChapter:PERIODIC PROPERTIESExercise:MATCH THE COLUMN
Explore 11 Videos
- s-BLOCK ELEMENTSBook:VK JAISWAL ENGLISHChapter:s-BLOCK ELEMENTSExercise:SUBJECTIVE PROBLEMS
Explore 2 Videos
Similar Questions
Knowledge Check
The molar solubility (in mol L−1) of a sparingly soluble salt MX4 is 's' The corresponding solubility product is Ksp .s is given in terms of Ksp by the relation.
As=(Ksp128)1/4Bs=(128Ksp)1/4Cs=(256Ksp)1/5Ds=(Ksp256)1/5For a sparingly soluble salt ApBq, the relationship of its solubility product (Ks) with its solubility (S) is
AKs=Sp+q.Pp.qqBKs=Sp+q.Pq.qpCKs=Spq.pp.qqDKs=Spq,(pq)p+qThe solubility of BaSO4 in water is 2.42×10−3gL−1 at 298 K. The value of its solubility product (Ksp) will be (Given molar mass of BaSO4=233g mol−1)
A1.08×10−10mol2L−2B1.08×10−12mol2L−2C1.08×10−14mol2L−2D1.08×10−8mol2L−2
Correct order of solubility of given compounds in water is
View SolutionpH of saturated solution of Ba(OH)2 is 12. The value of solubility product (Ksp) of Ba(OH)2 is
View SolutionThe solubility product (Ksp) of the following compound are given at 25∘C
The most soluble and least soluble compound are :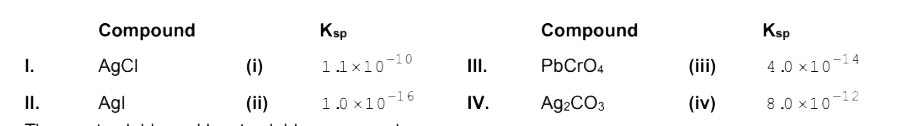
View SolutionThe product of the concentration of the ions of an electrolyte raised to power of their coefficients in the balanced chemical equation in the solution at any concentration . Its value is not constant and varies with change in concentration . Its value is not constant and varies with change in concentration . Its value is not constant and varies with change in concentration . Ionic product of the saturated solution is called solubility product Ksp
(i) When Kip=Ksp , the solution is just saturated and no precipitation takes place .
(ii) When Kip<Ksp the solution is unsaturated and precipitation will not take place .
(iii) When Kip>KsP the solution is supersaturated and precipitation takes place .
The solubility product Ksp , of sparingly soluable salt MX at 25∘ is 2.5×10−9 . The solubility of the salt in mol L−1 at this temperature is :
View SolutionA solution which remains in equilibrium with undissolved solute is said to be saturated. The concentration of a saturated solution at a given temperature is called solubility. The product of concentration of ions in a saturated solution of an electrolyte at a given temperature, is called solubility product (Ksp). For the electrolyte, Ax,By,:Ax,By(s)→xAy++yBx−, with solubility S, the solubility product (Ksp)=xx×yy×sx+y. While calculating the solubility of a sparingly soluble salt in the presence of some strong electrolyte containing a common ion, the common ion concentration is practically equal to that of strong electrolyte. If in a solution, the ionic product of an clectrolyte exceeds its Ksp, value at a particular temperature, then precipitation occurs.
The solubility of BaSO4, in 0.1 M BaCl2, solution is (Ksp, of BaSO4,=1.5×10−9)
View Solution

