If A=∫π0sinxx2dx, then ∫π/20cos2xxdx is equal to:
A
1−A
B
32−A
C
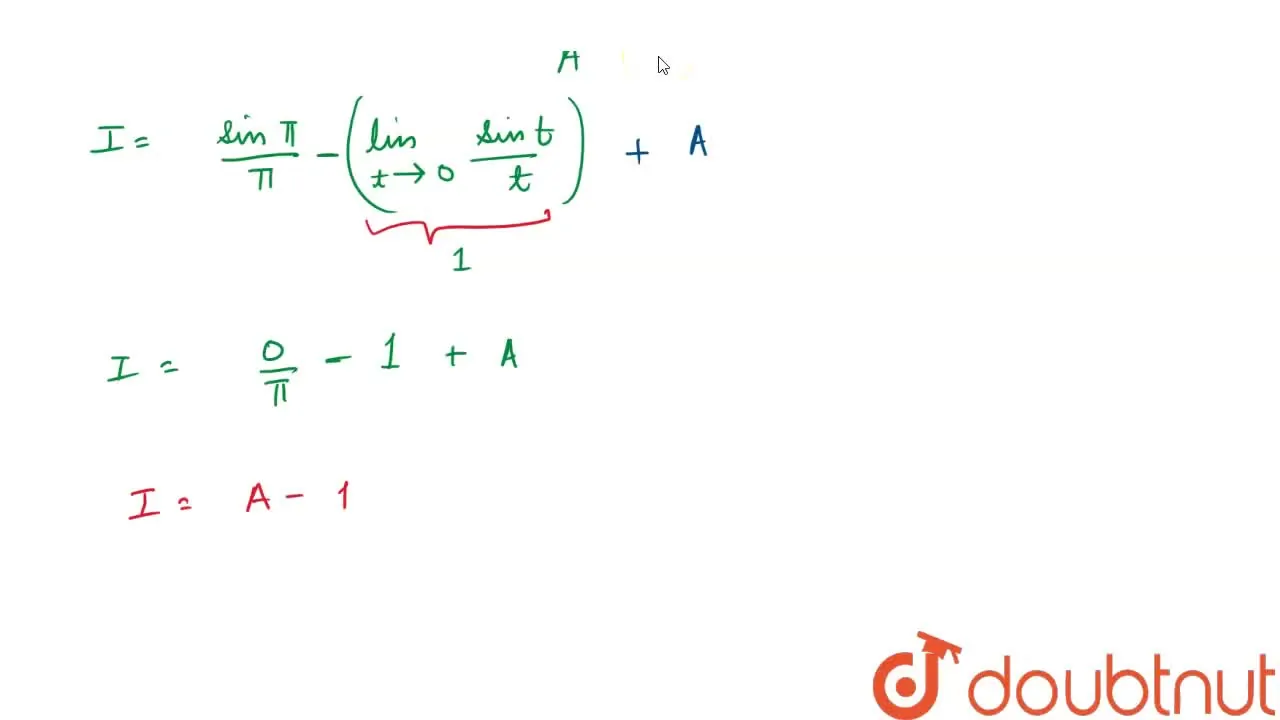
A−1
D
1+A
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video & image solution for If A= int _(0)^(pi) (sin x)/(x ^(2))dx, then int _(0)^(pi//2) (cos 2 x )/(x) dx is equal to: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - INDEFINITE AND DEFINITE INTEGRATIONEXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)16videos
INDEFINITE AND DEFINITE INTEGRATION
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - INDEFINITE AND DEFINITE INTEGRATIONEXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)14videos
INDEFINITE AND DEFINITE INTEGRATION
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise-4 : Subjective Type Problems3videos
HYPERBOLA
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNTIONS EXERCISE - Exercise-5 : Subjective Type Problems5videos
INVERSE TRIGONOMETRIC FUNTIONS
Similar Questions
∫π0[2sinx]dx=
View Solution∫π20cos2xdx
View SolutionIf ∫∞0cosxxdx=π2,then∫∞0cos3xxdx is equals to:
View Solution∫π/20x2cosxdx
View Solution∫π0xsinxcos2x dx
View Solution∫2π0sin2xdx
View Solution∫π/20sin2xdx
View SolutionIf A=∫π0cosx(x+2)2 dx, then ∫π/20sin2xx+1 dx is equal to
View Solution∫π/20sinxcosx1+sinxdx is equal to
View SolutionThe integral ∫π/20f(sin2x)sinxdx is equal to
View Solution