The coefficient of correlation for the variables x and y is 0.9926 from following data :
X182025303132Y212228323536
Find the change in the correlation coefficient if each value of x in multiplied b 3 and subtracted by 4 and each value of y is multiplied by 2 and increased by 3.
The correct Answer is:No change
To solve the problem, we need to determine the change in the correlation coefficient when the values of x and y are transformed. The original correlation coefficient is given as r=0.9926.
Step 1: Understand the transformations
The transformations applied to the variables are:
- For x: Multiply by 3 and subtract 4, which can be expressed as x′=3x−4.
- For y: Multiply by 2 and add 3, which can be expressed as y′=2y+3.
Step 2: Analyze the effect of transformations on correlation
The correlation coefficient r is invariant under linear transformations of the form ax+b and cy+d. Specifically:
- If x is transformed to x′=ax+b and y is transformed to y′=cy+d, the new correlation coefficient r′ will be given by:
r′=r⋅a⋅c|a|⋅|c|=r
This means that the correlation coefficient remains unchanged if both transformations are linear.
Step 3: Identify the constants in the transformations
In our case:
- For x: a=3 (the multiplier), and b=−4 (the constant added).
- For y: c=2 (the multiplier), and d=3 (the constant added).
Step 4: Calculate the new correlation coefficient
Since both transformations are linear, the correlation coefficient will not change:
r′=r=0.9926
Step 5: Conclusion
Thus, the change in the correlation coefficient is:
Δr=r′−r=0.9926−0.9926=0
Final Answer
The change in the correlation coefficient is 0.
---
The transformations applied to the variables are:
- For x: Multiply by 3 and subtract 4, which can be expressed as x′=3x−4.
- For y: Multiply by 2 and add 3, which can be expressed as y′=2y+3.
The correlation coefficient r is invariant under linear transformations of the form ax+b and cy+d. Specifically:
- If x is transformed to x′=ax+b and y is transformed to y′=cy+d, the new correlation coefficient r′ will be given by:
r′=r⋅a⋅c|a|⋅|c|=r
This means that the correlation coefficient remains unchanged if both transformations are linear.
In our case:
- For x: a=3 (the multiplier), and b=−4 (the constant added).
- For y: c=2 (the multiplier), and d=3 (the constant added).
Since both transformations are linear, the correlation coefficient will not change:
r′=r=0.9926
Thus, the change in the correlation coefficient is:
Δr=r′−r=0.9926−0.9926=0
The change in the correlation coefficient is 0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the regression coefficients y on x and x on y respectively are 0.8 and 0.2, what would be the value of coefficient of correlation?
A1.6B0.4C0.1DNone of these
The coefficient of correlation between the values denoted by x and y is 0.5. The standard deviation of x is 5 and that of y is 4. Find the angle between the lnes of regression.
View SolutionFind the coefficient of correlation, when Cov(x, y) = -16.5, Var(x)= 100, Var(y)=2.89.
View SolutionCalculate Kari Pearson's coefficient of correlation between the values of x and y for the following data :
n=10,∑x=55,∑y=40,∑x2=385,∑y2=192and∑(x+y)2=947
View SolutionIf x+y=12 and xy=32, find the value of x2+y2.
View SolutionCaculate Karl Pearson 's coefficient of correlation between X and Y from the following data :

Assume 80 and 130 as the mean values for X and Y respectively .
View SolutionIf two lines of regression are 4x+2y−3=0and3x+6y+5=0, then find the correlation coefficient.
View SolutionYou are given the following data:
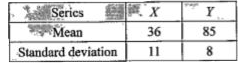
Correlation coefficient between x and y=0.66. Find the equations of the lines of regression.
View Solution


