Let n be a positive integer with f(n)=1!+2!+3!+….+n! and P(x) and Q(x) be polynomials in x such that f(n+2)=Q(n)f(n)+P(n)f(n+1). Find P(2).Solution in Bengali
P(x)=x+3
Q(x)=-1+2
P(X)=-1-2
Q(x)=x+3
The correct Answer is:A
Step by step video, text & image solution for Let n be a positive integer with f(n)=1!+2!+3!+….+n! and P(x) and Q(x) be polynomials in x such that f(n+2) = Q(n)f(n) + P(n)f(n+1). Find P(2). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If y=tan−1(x3) then dy/dx=
View SolutionLet the question f(x)=logx2 and ϕ(x)=2logx, then
View SolutionIf f(x)=(p-x^(n))^((1)/(n)),p>0 and n is a positive integer then f[f(x)] is equal to
View SolutionLet (5 + 2sqrt6)^n= p+ f , where n in N and p in N and 0
View SolutionLet n be a positive integer with f(n)=1!+2!+3!+.........+n!andp(x),Q(x) be polynomial in x such that f(n+2)=P(n)f(n+1)+Q(n)f(n) for all n≥, Then
View SolutionLet limx→∞n12(1+1n).(11.22.33....nn)1n2=e−pq
where p and q are relative prime positive integers. Find the vlaur of |p+q|.
View SolutionIf f(x)=(a−xn)1n,a>0 and n is a positive integer, then prove that f(f(x)) = x.
View SolutionIf f(x)=(p-x^(n))^(1//n), p gt 0 and n is a positive integer, then f[f(x)] is equal to
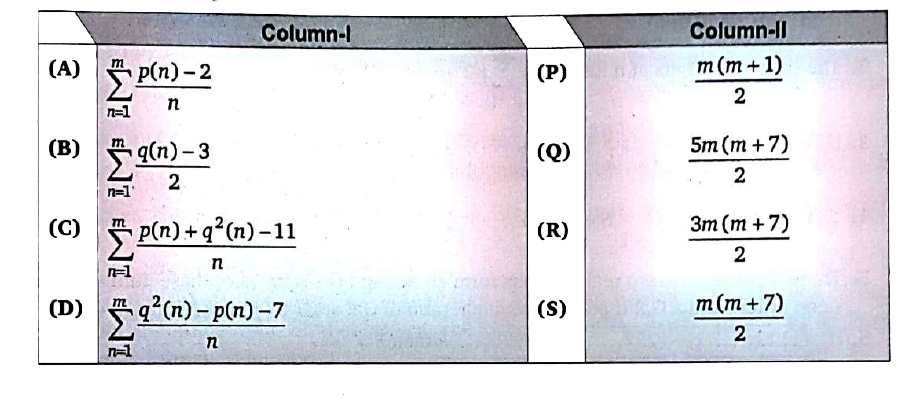
View SolutionLet f(x)=1+12+13+14+………+1n such that P(n)f(n+2)=P(n)f(n)+q(n). Where P(n)Q(n) are polynomials of least possible degree and P(n) has leading coefficient unity. Then match the following Column-I with Column-II.
View Solutiona>0,n= ধনাত্মক পূর্ণসংখ্যা এবং f(x)=(a−xn)1n হলে, দেখাও যে, f[f(x)]=x ।
View SolutionIf f(x)=(p−xn)1n ,p>0 andn is a positive integer then f[f(x)] is equal to
View SolutionLet f:N→N be defined by f(x)=x2+x+1,x∈N. Then f is
View SolutionLet n be a positive integer with f(n)=1!+2!+3!+.........+n!andp(x),Q(x) be polynomial in x such that f(n+2)=P(n)f(n+1)+Q(n)f(n) for all n≥, Then
View SolutionIf f(x)=(p−xn)1n,p>0 and n is positive integer, then the value of f[f(x)]
View SolutionLet limx→∞n12(1+1n).(11.22.33....nn)1n2=e−pq
where p and q are relative prime positive integers. Find the value of |p+q|.
View Solution
