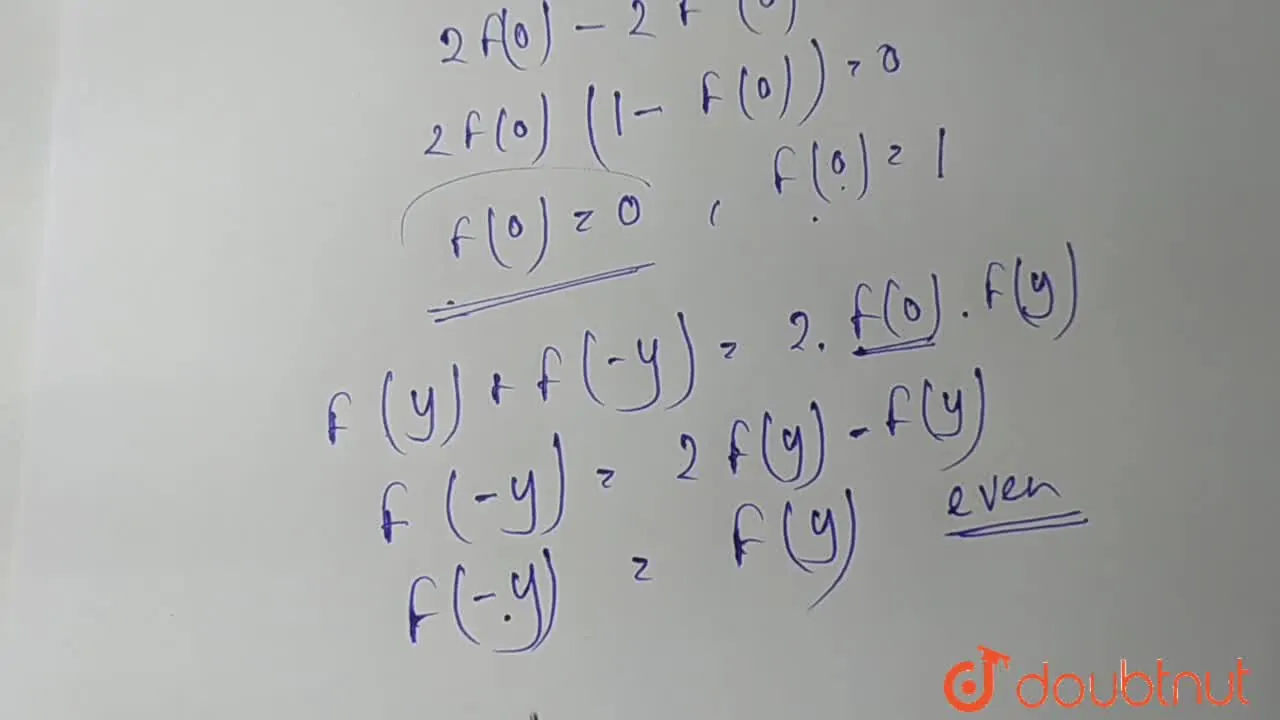If f(x+y)+f(x-y)=2f(x).f(y)∀x,y∈R. f(0)≠0, find if f(x) is even or odd function.Solution in Bengali
f(x+y)+f(x-y)=2f(x)f(y)
put x=y=0
2f(0)=(f(0))2⇒f(0)=0orf(0)=1<br>givenf(0)ne0.Hencef(0)=1<br>Aga∈puty=x,andx=0<br>f(x)+f(-x)=2f(0)f(x)
f(x)+f(-x)=2f(x)
∴ f(x)=f(-x)
Hence the function f(x) is an even function.
Related Playlists
Similar Questions
If y=tan−1(x3) then dy/dx=
02:12View SolutionLet the question f(x)=logx2 and ϕ(x)=2logx, then
03:27View SolutionProve that f(x)givenbyf(x+y)=f(x)+f(y)∀x∈R is an odd function.
03:10View SolutionIf the function / satisfies the relation f(x+y)+f(x−y)=2f(x),f(y)∀x,y∈Randf(0)≠0 , then f(x)isa≠venfunction f(x)isanoddfunction Iff(2)=a,thenf(−2)=a Iff(4)=b,thenf(−4)=−b
02:33View SolutionLet f(x+(1)/(y))+f(x-(1)/(y))=2f(x)f((1)/(y))AA x,y in R,y!=0 and f(0)=0 then the value of f(1)+f(2)=
05:05View SolutionIf f(x) is a function satisfying f(x)-f(y)=(y^(y))/(x^(x))f((x^(x))/(y^(y)))AA x,y in R^(*) and f'(1)=1, then find f(x)
04:54View SolutionLet f(x+y)+f(x-y)=2f(x)f(y)AA x,y in R and f(0)=k, then
02:18View SolutionLet f(x+y) + f(x-y) = 2f(x)f(y) for x, y∈R and f(0)≠0. Then f(x) must be
02:47View SolutionIf a function f satisfies the conditions f(x+y)=f(x)+f(y)∀,x,y∈R, then f is :
02:13View SolutionIf f ne 0 The real function is such that f (x + y) + f (xy) = 2f (x) .f (y), AA x, y in R , Then f (x) is
05:28View Solutionमाना f(x+y)+f(x-y)=2f (x)f(y) , AA x , y in R And f(0) ne 0 , Then the function is f (x)
02:50View SolutionLet f(x+1y)+f(x−1y)=2f(x)f(1y)∀x,y∈R,y≠0 and f(0)=0 then the value of f(1)+f(2)=
04:20View Solutionवक्तव्य I - यदि f(x+y)+f(x−y)=2.f(x).f(y),∀x,y∈R तथा f(0)≠0, तो f(x) सम फलन होगा।
वक्तव्य II - यदि f(−x)=f(x),∀x, तब f (x) सम फलन होगा।03:38View Solutiony=f(x), Where f satisfies the relation f(x+y)=2f(x)+xf(y)+y√f(x)∀x,y∈R and f'(0)=0. Then f(6) is equal to ………
06:45View SolutionLet f(x+y) + f(x-y) = 2f(x)f(y) for x, y∈R and f(0)≠0. Then f(x) must be
01:57View Solution