Let A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1, A0A2 and A0A4 isSolution in Bengali
The correct Answer is:C
Step by step video & text solution for Let A_0A_1A_2A_3A_4A_5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A_0A_1, A_0A_2 and A_0A_4 is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If A={x:x=4n+1,n≤5 and n∈N} and B={3n:n≤8andn∈N} then (A-B) is
View SolutionFor a frequency distribution, mean deviation about mean is computed by
View Solution. Find the length of the side of a regular hexagon inscribed in a circle of radius r meters
View SolutionLet X,Y,Z be respectively the areas of regular pentagon, regular hexagon and regular heptagon which are inscribed in a circle of radius 1. Then
View SolutionWhat is the difference in the areas of the regular hexagon circumscribing a circle of radius 10 cm and the regular hexagon inscribed in the circle?
View SolutionA regular hexagon is inscribed in a circle of radius 5 cm. If x is the area inside the circle but outside the regular hexagon, then which one of the following is correct?
View SolutionIf a regular hexagon is inscribed in a circle of radius r, then find the perimeter of the hexagon.
View SolutionIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
View SolutionA regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
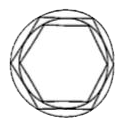
What is the ratio of area of inner circle to the outer circle ?
View SolutionA0,A1,A2,A3,A4,A5 be a regular hexagon inscribed in a circle of unit radius ,then the product of (A0A1⋅A0A2⋅A0A4 is equal to
View SolutionLet A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths the line segments A0A1,A0A2 and A0A4 is
View SolutionLet A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths the line segments A0A1,A0A2 and A0A4 is
View SolutionLet A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1,A0A2,A0A4 is
View SolutionIf a regular hexagon is inscribed in a circle of radius r , then its perimeter is :
View SolutionLet A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1, A0A2 and A0A4 is
View SolutionA0,A1,A2,A3,A4,A5 be a regular hexagon inscribed in a circle of unit radius ,then the product of (A0A1⋅A0A2⋅A0A4 is equal to
View Solution
