A wire ring of diameter 0.03m is dipped in a liquid and pulled out gently. If a force of 0.1N is required to break the film, then what is the surface tension of the liquid?
The correct Answer is:0.52Nm−1
To find the surface tension of the liquid, we can follow these steps:
Step 1: Identify the Given Values
- Diameter of the wire ring (d) = 0.03 m
- Force required to break the film (F) = 0.1 N
Step 2: Calculate the Radius of the Ring
The radius (r) is half of the diameter:
r=d2=0.03m2=0.015m
Step 3: Calculate the Circumference of the Ring
The circumference (C) of the ring is given by the formula:
C=2πr
Substituting the value of r:
C=2π(0.015m)=0.09424778m≈0.0942m
Step 4: Use the Formula for Surface Tension
The surface tension (T) is defined as the force (F) divided by the length (C):
T=FC
Substituting the values we have:
T=0.1N0.0942m≈1.06N/m
Final Answer
The surface tension of the liquid is approximately:
T≈1.06N/m
---
- Diameter of the wire ring (d) = 0.03 m
- Force required to break the film (F) = 0.1 N
The radius (r) is half of the diameter:
r=d2=0.03m2=0.015m
The circumference (C) of the ring is given by the formula:
C=2πr
Substituting the value of r:
C=2π(0.015m)=0.09424778m≈0.0942m
The surface tension (T) is defined as the force (F) divided by the length (C):
T=FC
Substituting the values we have:
T=0.1N0.0942m≈1.06N/m
The surface tension of the liquid is approximately:
T≈1.06N/m
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 2(SURFACE TENSIONS) FROM CAPILLARY
Explore 15 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 3 (KINETIC THEORY OF GASES ) CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
Explore 5 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 2(SURFACE TENSIONS)VERY SHORT ANSWER QUESTIONS
Explore 13 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
- SAMPLE QUESTION PAPER - 01 Book:ICSEChapter:SAMPLE QUESTION PAPER - 01 Exercise:SECTION - D
Explore 12 Videos
Similar Questions
A ring of internal and external diameters 8.5×10−2m and 8.7×10−2m is supported horizontally from the pan of a physical balance such that it comes in contact with a liquid. An extra force of 40N is required to pull it away from the liquid . Determine the surface tension of the liquid?
View SolutionThe ring of radius 1 m is lying on the surface of liquid. It is lifted. It is lifted from the liquid surface by a force of 4 newtons in such a way that the liquid film in it remains intact. The surface tension of liquid will be
View Solution
Knowledge Check
A square wire fram of size L is dipped in a liquid. On taking out a membrane is formed. Ifthe surface tension of the liquid is T, the force acting on the frame will be
A2 T LB4 T LC8 T LD10 T L
A square wire fram of size L is dipped in a liquid. On taking out a membrane is formed. Ifthe surface tension of the liquid is T, the force acting on the frame will be
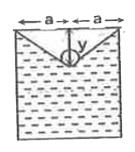
View SolutionA long wire of negligible thickness and mass per unit length λ is floating in a liquid such that the top surface of liquid dips by a distance 'y' If the lendth of base of vessel is 2a , find surface tension of the liquid (y>>a)
View SolutionA very light, rectangular wire-frame of dimensions 7cm×5cm hangs just above the free surface of a liquid of surface tension T, with its plane parallel to the free surface. The wire -frame is just brought in contact with the liquid surface and then, lifted up. If the force required to lift the wire-frame is 3.36 N, then what is the value of T in (Nm−1)?
View Solution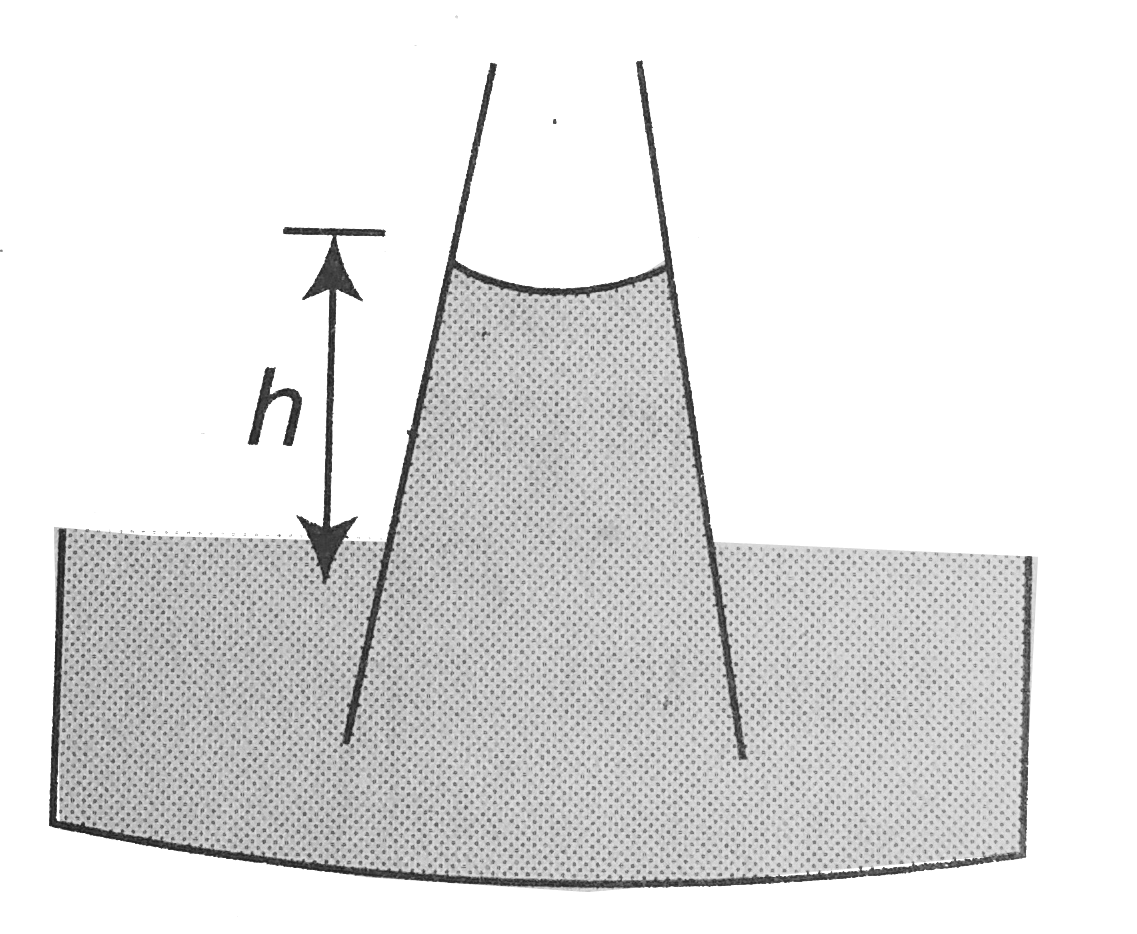
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionWhen a long capillary tube of radius 0.015 cm is dipped in a liquid, the liquid rises to a height of 15 cm within it. If the contact angle between the liquid and glass to close to 0∘, the surface tension of the liquid, in milliNewton m−1, is [ρliquid=900kgm−3,g=10ms−2] (give anwer is closet integer)
View SolutionA wire 0.1m long is placed horizontally on the surface of water and is gently pulled up with a force of 1.456×10−2N to keep the wire in equilibrium. Calculate the surface tension of water.
View SolutionA container of width 2a is filled with a liquid. A thin wire of weight per unit length λ is gently placed over the liquid surface in the middle of the surface as shown in the figure. As a result, the liquid surface is depressed by a distance y(y<<a). If the surface tension of the liquid is 4λagky. Then value of k is .

View Solution

