A cable is cut to half of its original length. Why does this change has no effect on the maximum load that it can support?
To understand why cutting a cable to half of its original length does not affect the maximum load it can support, we can analyze the concepts of stress and breaking stress.
1. Understanding Stress:
- Stress is defined as the force applied per unit area. Mathematically, it is given by:
Stress=ForceArea
2. Breaking Stress:
- The breaking stress of a material is the maximum stress that it can withstand before failing. It is a property of the material and does not depend on the dimensions of the object (length, width, etc.).
3. Maximum Load Calculation:
- The maximum load (F_max) that a cable can support before breaking can be expressed as:
Fmax=Breaking Stress×Cross-sectional Area
- Here, the breaking stress is a constant for a given material, and the cross-sectional area is the area of the cable's cross-section.
4. Effect of Cutting the Cable:
- When the cable is cut to half its original length, the length of the cable changes, but the cross-sectional area remains the same. Therefore, the breaking stress remains unchanged as it is a material property.
5. Conclusion:
- Since the maximum load is determined by the breaking stress and the cross-sectional area, and since neither of these factors changes when the cable is cut in half, the maximum load that the cable can support remains the same. Thus, cutting the cable does not affect its maximum load capacity.
Final Answer:
The maximum load that a cable can support is independent of its length; it depends only on the breaking stress and the cross-sectional area. Therefore, cutting the cable to half its original length has no effect on the maximum load it can support.
---
- Stress is defined as the force applied per unit area. Mathematically, it is given by:
Stress=ForceArea
- The breaking stress of a material is the maximum stress that it can withstand before failing. It is a property of the material and does not depend on the dimensions of the object (length, width, etc.).
- The maximum load (F_max) that a cable can support before breaking can be expressed as:
Fmax=Breaking Stress×Cross-sectional Area
- Here, the breaking stress is a constant for a given material, and the cross-sectional area is the area of the cable's cross-section.
- When the cable is cut to half its original length, the length of the cable changes, but the cross-sectional area remains the same. Therefore, the breaking stress remains unchanged as it is a material property.
- Since the maximum load is determined by the breaking stress and the cross-sectional area, and since neither of these factors changes when the cable is cut in half, the maximum load that the cable can support remains the same. Thus, cutting the cable does not affect its maximum load capacity.
The maximum load that a cable can support is independent of its length; it depends only on the breaking stress and the cross-sectional area. Therefore, cutting the cable to half its original length has no effect on the maximum load it can support.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)FROM YOUNG.S MODULUS
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM BULK MODULUS
8 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)SHORT ANSWER QUESTIONS
20 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
A wire is replaced by another wire of same length and material but of twice diameter.
(i) What will be the effect on the increases in its length under a given load?
(ii) What will be the effect on the maximum load which it can bear?
View SolutionA cable that can support a load W is cut into two equal parts .T he maximum load that can be supported by either part is
View Solution
Knowledge Check
A cylindrical rod is reformed to half of its original length keeping volume constant. If its resistance before this change were R, then the resistance after reformation of rod will be
ARBR/4C3R/4DR/2A steel cable with a radius 2 cm supports a chairlift at a ski area. If the maximum stress is not to exceed 108Nm−2, the maximam load the cable can support
A4π×105NB4π×104NC2π×105ND2π×104
If a thin lens is dipped in water, does its focal length change ?
View SolutionA wire of resistance(10Ω) is stretched to twice its original length. The resistance of half of the streached wire is
View SolutionA steel cable with a radius of 1.5 cm support a chairlift at a ski area.if the maximum stress is not to exceed 108Nm−2, what is the maximum load the cable can support?
View SolutionA block of weight W produces an extension of 9cm when it is hung by an elastic spring of length of 60cm and is in equilibrium. The spring is cut into two parts, one of length 40cm and the other of length 20cm. The same load W hangs in equilibrium supported by both parts as shwon in figure. The extension in cm noe is
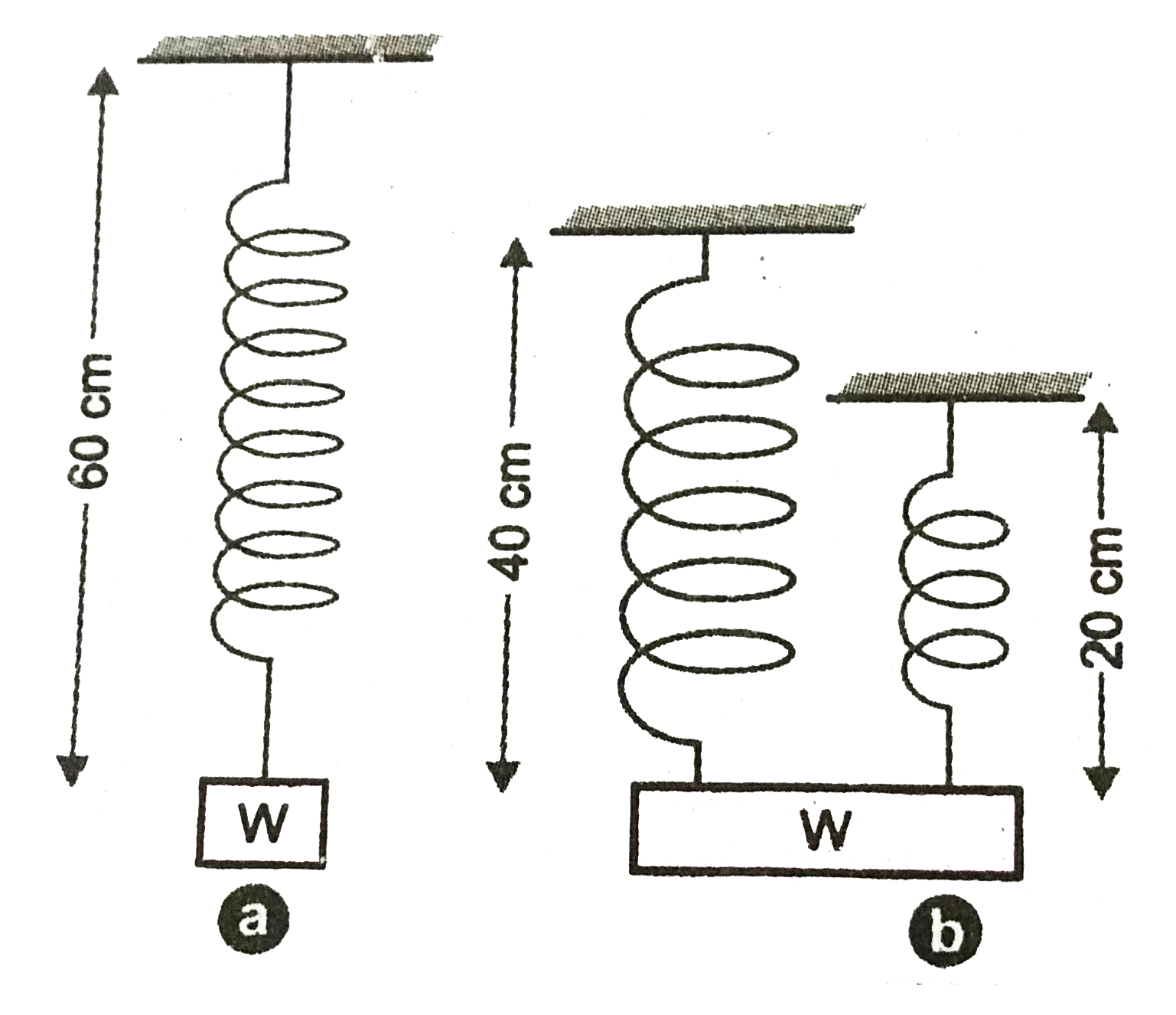
View SolutionA block of weight W produces an extension of 9cm when it is hung by an elastic spring of length of 60cm and is in equilibrium. The spring is cut into two parts, one of length 40cm and the other of length 20cm. The same load W hangs in equilibrium supported by both parts as shwon in figure. The extension in cm noe is

View SolutionA heater coil is cut into two parts of equal length and one of them is used in the leader. The ratio of the heat procued by this half coil to that by the original coil is
View Solution
