how will you combine →Eand→A such that their vector sum is
(i) →A (ii) →E (iii) 2→A
(i) →E+2→A (ii) →A+2→E (iii) →E+3→A
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:FROM UNIT VECTORS COMPONENTS OF A VECTOR
Explore 6 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:FROM SCALAR PRODUCT AND VECTOR PRODUCT
Explore 20 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:VERY SHORT ANSWER QUESTIONS
Explore 10 Videos
- UNITSBook:ICSEChapter:UNITSExercise:MODULE 3 (SELECTED PROBLEMS)
Explore 38 Videos
- WAVESBook:ICSEChapter:WAVESExercise:From Musical Sound
Explore 10 Videos
Similar Questions
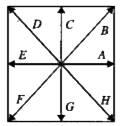
A number of vectors are as shown in .They can be combined in various ways , like →A+→C=→B . What is the value of (a) →E+→C (b) →A+→F (c ) →A+→D (d) →E+→A (e ) →A−→B .
View SolutionIf →a→b→cand→d are vectors such that →a×→b=→c×→dand→a×→c=→b×→d. Then show that the vectors →a−→d and →b−→c are parallel.
View Solution→Aand→B are two vectors having the same magnitude . What is the condition that (i) the vector sum →A+→B and (ii) the vector differece →A+→B have the same magnitude as →Aand→B ?
View SolutionA charged particle goes undeflected in a region containing electric and magnetic field. It is possible that
(i) →E∣∣∣∣→B.→v∣∣∣∣→E
(ii) →E is not parallel to →B
(iii) →v∣∣→B but →E is not parallel to →B
(iv) →E∣∣→B but →v is not parallel to →E
View SolutionIf V=2r2 then find (i) →E(1,0,−2) (ii) →E(r=2)
View SolutionIf two vectors →aand→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣, then find the angle the vectors →aand→b
View SolutionIf there are two vectors →A and →B such that →A+→B=ˆi+2ˆj+ˆk and →A−→B=(ˆi−→k), then choose the correct options.
View SolutionIf →A,→Band→C are three vectors when you can say that →A+→B=→CandA+B=C are the same ?
View SolutionShow that the magnitude of vector sum of →aand→b cannot be greater than |→a|+∣∣→b∣∣ or smaller than |→a|−∣∣→b∣∣
View SolutionThree vector →A,→B, →C satisfy the relation →A⋅→B=0and →A.→C=0. The vector →A is parallel to
View Solution

