What is the condition under which the magnitude of cross product is equal to the dot product ?
To determine the condition under which the magnitude of the cross product of two vectors is equal to the dot product of the same two vectors, we can follow these steps:
1. Define the Vectors: Let the two vectors be →A and →B.
2. Write the Formulas:
- The magnitude of the cross product |→A×→B| is given by:
|→A×→B|=|→A||→B|sinθ
- The dot product →A⋅→B is given by:
→A⋅→B=|→A||→B|cosθ
3. Set the Magnitudes Equal: We want to find the condition when these two magnitudes are equal:
|→A||→B|sinθ=|→A||→B|cosθ
4. Cancel Common Terms: Assuming |→A| and |→B| are non-zero, we can divide both sides by |→A||→B|:
sinθ=cosθ
5. Use Trigonometric Identity: We can rewrite the equation as:
sinθcosθ=1
This simplifies to:
tanθ=1
6. Find the Angle: The angle θ for which tanθ=1 is:
θ=45∘orθ=π4 radians
Conclusion:
The condition under which the magnitude of the cross product is equal to the dot product is when the angle θ between the two vectors →A and →B is 45∘ or π4 radians.
---
- The magnitude of the cross product |→A×→B| is given by:
|→A×→B|=|→A||→B|sinθ
- The dot product →A⋅→B is given by:
→A⋅→B=|→A||→B|cosθ
|→A||→B|sinθ=|→A||→B|cosθ
sinθ=cosθ
sinθcosθ=1
This simplifies to:
tanθ=1
θ=45∘orθ=π4 radians
The condition under which the magnitude of the cross product is equal to the dot product is when the angle θ between the two vectors →A and →B is 45∘ or π4 radians.
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:SELECTED PROBLEMS (FROM VECTOR ADDITION )
Explore 14 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:FROM UNIT VECTORS COMPONENTS OF A VECTOR
Explore 6 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:SHORT ANSWER QUESTIONS
Explore 44 Videos
- UNITSBook:ICSEChapter:UNITSExercise:MODULE 3 (SELECTED PROBLEMS)
Explore 38 Videos
- WAVESBook:ICSEChapter:WAVESExercise:From Musical Sound
Explore 10 Videos
Similar Questions
What is the condition under which Hooke's law holds goods?
View SolutionUnder what condition the magnitude of average velocity is equal to the average speed ?
View SolutionMass of products is equal to mass of reactants.
View SolutionWhat is the condition for magnitude of →A+→B to be equal to that of →A−→B ?
View SolutionMagnitude of primary productivity is affected by
View SolutionAldehyde and ketones may be prepared by reductive cleavage of carbon-carbon double bonds. A particularly useful reagent for this purpose is ozone under reductive condition in the formation of carbonyl compounds.
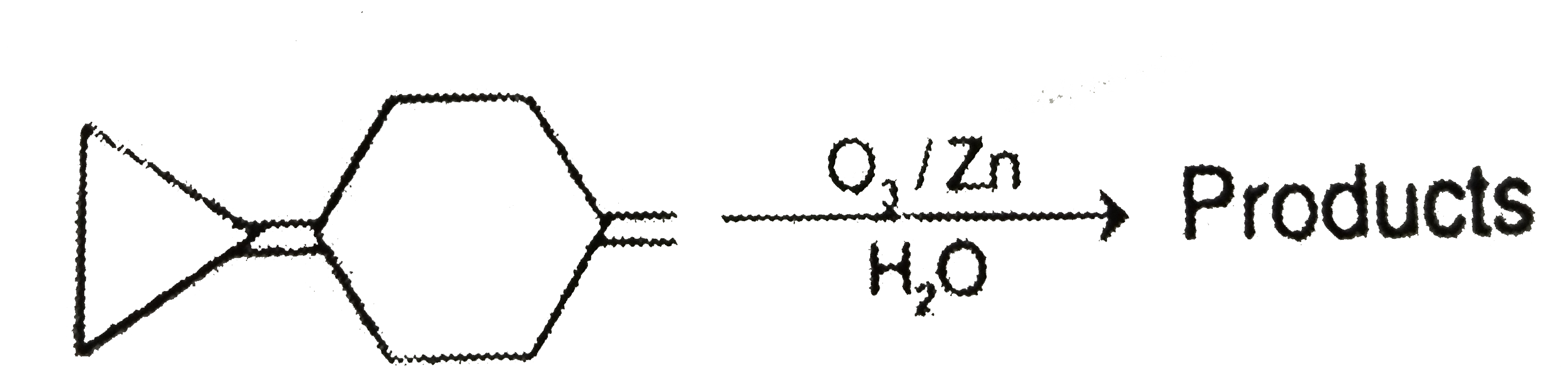 products
products
Which of the following products is not formed in above reaction.
View SolutionUnder what conditions (s) is the magnitude of average velocity of an object equal to its average speed ?
View SolutionUnder what conditions (s) is the magnitude of average velocity of an object equal to its average speed ?
View SolutionIf two vectors are represented by the two sides of a triangle , then show that half the magnitude of their cross product will give the area of the triangle .
View SolutionOnly biotic factors affect the magnitude of primary productivity.
View Solution

