P,Q and R are three forces acting simultaneously on a particle . is the vector sum, of the three forces show that if = 0 , the vector representing these forces form a triangle.
To prove that if the vector sum of three forces →P,→Q,→R acting on a particle is zero, then these vectors form a triangle, we can follow these steps:
Step 1: Understand the Given Information
We are given three forces →P,→Q,→R acting on a particle. The vector sum of these forces is represented as:
→S=→P+→Q+→R
It is given that →S=0.
Step 2: Rewrite the Equation
From the equation →S=0, we can rearrange it to show the relationship between the forces:
→P+→Q+→R=0⟹→P+→Q=−→R
Step 3: Interpret the Result
The equation →P+→Q=−→R indicates that if we place the tail of vector →Q at the head of vector →P, the head of vector →Q will coincide with the tail of vector −→R. This means that the vectors →P,→Q, and →R can be arranged in such a way that they form a closed figure.
Step 4: Visualize the Triangle
To visualize this, we can represent the vectors:
- Start with vector →P.
- From the head of →P, draw vector →Q.
- The vector −→R can be drawn from the head of →Q back to the tail of →P.
This arrangement shows that the vectors form a closed loop, which is a triangle.
Step 5: Conclusion
Since the vectors →P,→Q, and →R can be arranged to form a closed figure, we conclude that if the vector sum of three forces acting on a particle is zero, then these vectors indeed form a triangle.
We are given three forces →P,→Q,→R acting on a particle. The vector sum of these forces is represented as:
→S=→P+→Q+→R
It is given that →S=0.
From the equation →S=0, we can rearrange it to show the relationship between the forces:
→P+→Q+→R=0⟹→P+→Q=−→R
The equation →P+→Q=−→R indicates that if we place the tail of vector →Q at the head of vector →P, the head of vector →Q will coincide with the tail of vector −→R. This means that the vectors →P,→Q, and →R can be arranged in such a way that they form a closed figure.
To visualize this, we can represent the vectors:
- Start with vector →P.
- From the head of →P, draw vector →Q.
- The vector −→R can be drawn from the head of →Q back to the tail of →P.
Since the vectors →P,→Q, and →R can be arranged to form a closed figure, we conclude that if the vector sum of three forces acting on a particle is zero, then these vectors indeed form a triangle.
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:EXAMPLES
Explore 26 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:Applications of integration in Physics
Explore 6 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:UNSOLVED PROBLEMS
Explore 79 Videos
- UNITSBook:ICSEChapter:UNITSExercise:MODULE 3 (SELECTED PROBLEMS)
Explore 38 Videos
- WAVESBook:ICSEChapter:WAVESExercise:From Musical Sound
Explore 10 Videos
Similar Questions
Knowledge Check
Let →F be a force acting on a particle having positon vector →r.Let→τ be the torque of this force about the origin then
A→r.→τ>0 and →F.→τ<0B→r.→τ=0 and →F.→τ=0C→r.→τ=0 and →F.→τ≠0D→r.→τ≠0 and →F.→τ=0
Three forces start acting simultaneously on a particle moving with velocity →v. These forces are represented in magnitude and direction by the three sides os a triangle ABC (as shown). The particle will now move with velocity.

View SolutionThree forces start acting simultaneously on a particle moving with velocity, →v. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
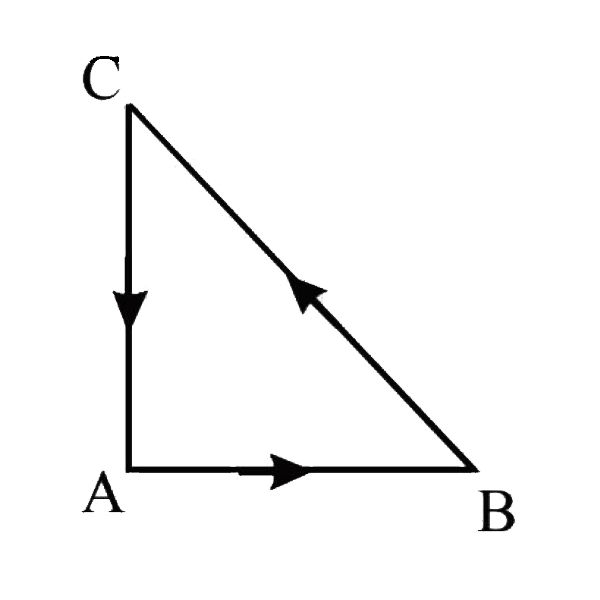
View SolutionA particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :

View SolutionLet →F be the force acting on a particle having position vector →rand→T be the torque of this force about the origin. Then
View Solutionif →a,→b,→c are three vectors such that →a+→b+→c=→0 then
View SolutionIf P,Q and R are three collinear points such that →PQ=→a and →QR = →b. Find the vector →PR .
View SolutionWrite the expression for the magnetic force →F acting on a charged particle q moving with →υ in the presence of the magnetic field →B in a vector form. Show that no work is done and no change in the magnitude of the velocity of the particle is produced by this force. Hence define the unit of magnetic field.
View Solution