Question

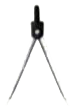
Name the geometrical instrument that has two legs, one with a pointed end and the other with a pencil/lead used for making geometrical constructions.

Answer

Compass

Explanation

Step-by-Step Solution:

1. Identify the Instrument: The question asks for a geometrical instrument that has two legs, one with a pointed end and the other with a pencil or lead.

2. Describe the Features: The instrument has one leg that is pointed, which is used to pivot or anchor the instrument on a point. The other leg holds a pencil or lead, which is used to draw.

3. Name the Instrument: Based on the description, the instrument that fits this criteria is called a "compass."

4. Usage of the Compass: A compass is commonly used in geometry for making constructions such as drawing circles, creating angles, and bisecting lines.

Final Answer: The geometrical instrument is called a "compass."

---