(a) Alpha particles having kinetic energy of 1.8 MeV each are incident on a thin gold foil , from a large distance. Applying the principle of conversation of energy, find the closest distance of approach of the alpha particle from the gold nucleus. (Atomic number of gold = 79).
To find the closest distance of approach of an alpha particle to a gold nucleus, we can use the principle of conservation of energy. The kinetic energy of the alpha particle will be converted into potential energy due to electrostatic repulsion when it gets close to the nucleus.
1. Identify Given Values:
- Kinetic Energy (KE) of the alpha particle: KE=1.8MeV=1.8×106eV
- Atomic number of gold (Z): Z=79
- Charge of an electron (e): e=1.6×10−19C
2. Convert Kinetic Energy to Joules:
KE=1.8×106eV×1.6×10−19J/eV=2.88×10−13J
3. Use the Formula for Potential Energy (PE):
The potential energy (PE) at the closest distance of approach r is given by:
PE=k⋅Z⋅2e2r
where k=9×109N m2/C2 is Coulomb's constant.
4. Set Kinetic Energy Equal to Potential Energy:
KE=PE⟹2.88×10−13=9×109⋅79⋅2⋅(1.6×10−19)2r
5. Rearranging for r:
r=9×109⋅79⋅2⋅(1.6×10−19)22.88×10−13
6. Calculating the Numerator:
Numerator=9×109⋅79⋅2⋅(1.6×10−19)2
=9×109⋅79⋅2⋅2.56×10−38
=9×79×2×2.56×10−29≈3640.32×10−29
7. Calculating r:
r=3640.32×10−292.88×10−13≈1.264×10−16m
8. Final Result:
r≈1.264×10−13m
Conclusion:
The closest distance of approach of the alpha particle to the gold nucleus is approximately 1.264×10−13m.
- Kinetic Energy (KE) of the alpha particle: KE=1.8MeV=1.8×106eV
- Atomic number of gold (Z): Z=79
- Charge of an electron (e): e=1.6×10−19C
KE=1.8×106eV×1.6×10−19J/eV=2.88×10−13J
The potential energy (PE) at the closest distance of approach r is given by:
PE=k⋅Z⋅2e2r
where k=9×109N m2/C2 is Coulomb's constant.
KE=PE⟹2.88×10−13=9×109⋅79⋅2⋅(1.6×10−19)2r
r=9×109⋅79⋅2⋅(1.6×10−19)22.88×10−13
Numerator=9×109⋅79⋅2⋅(1.6×10−19)2
=9×109⋅79⋅2⋅2.56×10−38
=9×79×2×2.56×10−29≈3640.32×10−29
r=3640.32×10−292.88×10−13≈1.264×10−16m
r≈1.264×10−13m
The closest distance of approach of the alpha particle to the gold nucleus is approximately 1.264×10−13m.
Similar Questions
In scattering experiment, find the distance of closest approach, if a 6MeVα−partic≤ is used
View SolutionCalculate distance of closet approach by an α-particle of KE=2.5MeV being scattered by gold nucleus (Z=79).
View SolutionDistance of closest approach when a 5.0MeV proton approaches a gold nucleus is (Z=79)
View SolutionDefine the distance of closest approach. An α-particle of kinetic enegy 'K' is bombarded on a thin gold foil. The distance of the closest approach is 'r' . What will be the distance of closest approach for an α-particle of double the kinetic energy ?
View Solution(a) Define the distance of closest approach. A α -particle of kinetic energy K is bombarded on a thin gld foil. The distance of the closest approach is ra. What will be the distance of closest approach for an α-particle of double the kinetic energy ?
(b) Show that the radius of the orbit of an electron in hydrogen atoms varies as n2, where n is the principal quantum number of the atom.
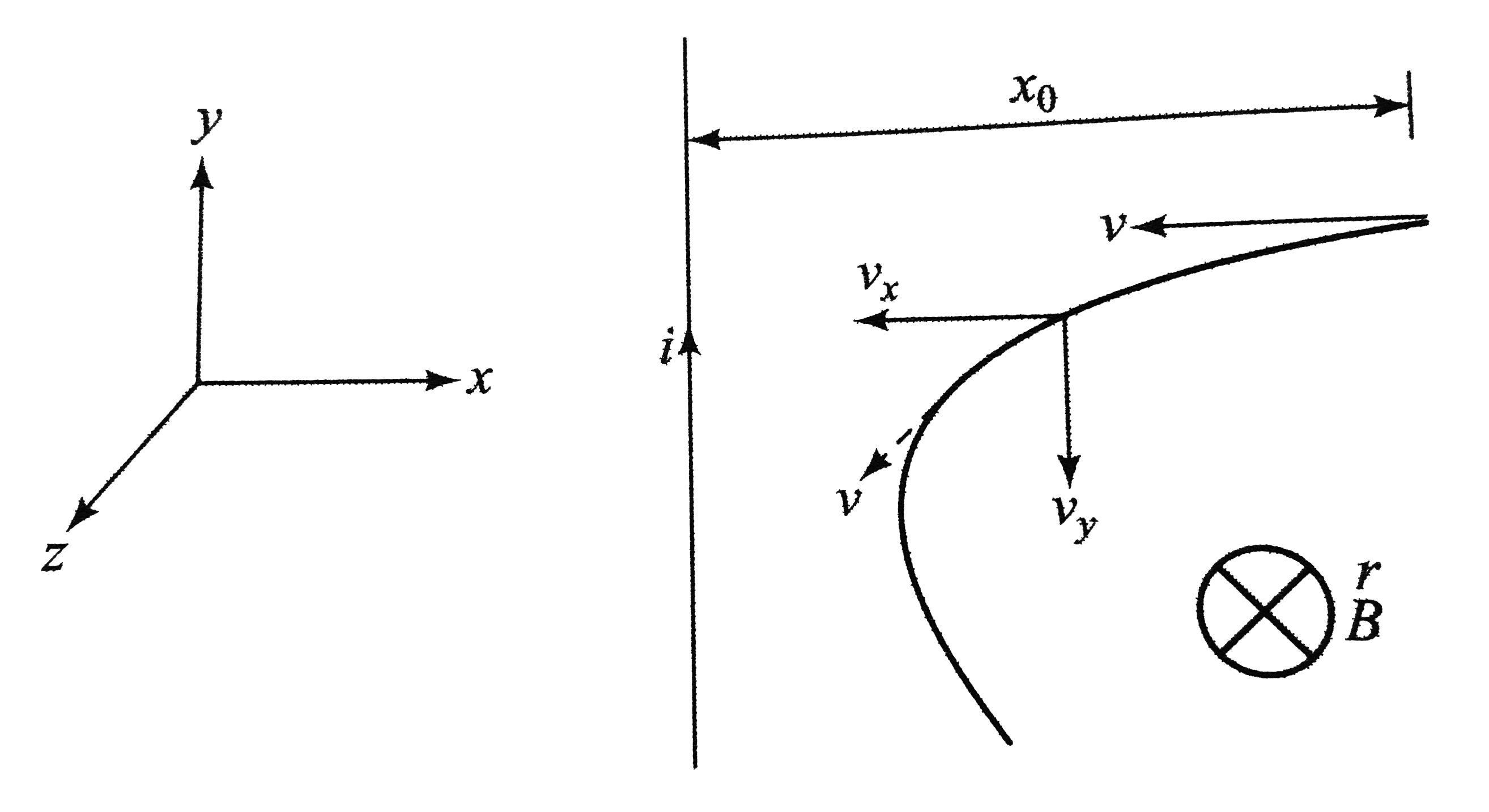
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionThe distance of closest approach of an α-particle fired at nucleus with momentum p is d. The distance of closest approach when the α-particle is fired at same nucleus with momentum 3p will be
View SolutionAn α - particle after passing through a potential difference of V volts collides with a nucleus . If the atomic number of the nucleus is Z then the distance of closest approach of α – particle to the nucleus will be
View SolutionAn alpha particle with kinetic energy 10MeV is heading toward a stationary tin nucleus of atomic number 50. Calculate the distance of closest approach (Fig . 3.23).
 .
.
View SolutionAn alpha particle with kinetic energy 10MeV is heading toward a stationary tin nuclcus of atomic number 50. Calculate the distance of closest approach (Fig . 3.23).
 .
.
View Solution
