The refractive indices of a material for red, violet and yellow colour lights are 1.52, 1.62 and 1.59 respectively. Calculate the dispersive power of the material. If the mean deviation is 40∘ what will be the angular dispersion produced by a prism of this material ?
To solve the problem step-by-step, we will first calculate the dispersive power of the material and then determine the angular dispersion produced by the prism.
Step 1: Calculate the Dispersive Power (Ω)
The formula for dispersive power is given by:
Ω=μV−μRμY−1
Where:
- μR=1.52 (refractive index for red light)
- μV=1.62 (refractive index for violet light)
- μY=1.59 (refractive index for yellow light)
Substituting the values into the formula:
Ω=1.62−1.521.59−1
Calculating the numerator and denominator:
Ω=0.100.59
Now, performing the division:
Ω≈0.169
Step 2: Calculate the Angular Dispersion
The mean deviation (D) is given as 40∘. The formula for mean deviation in terms of angular dispersion (A) is:
D=(μV−1)A+(μR−1)A+(μY−1)A3
Substituting the values of refractive indices:
40=(1.62−1)A+(1.52−1)A+(1.59−1)A3
This simplifies to:
40=(0.62A+0.52A+0.59A)3
Combining the terms in the numerator:
40=1.73A3
Multiplying both sides by 3:
120=1.73A
Now, solving for A:
A=1201.73≈69.4∘
Step 3: Calculate the Angular Dispersion
The angular dispersion (Δ) can be calculated using the formula:
Δ=(μV−μR)⋅A
Substituting the values:
Δ=(1.62−1.52)⋅A
This simplifies to:
Δ=0.10⋅A
Substituting the value of A:
Δ=0.10⋅1201.73
Calculating the final value:
Δ≈0.10⋅69.4≈6.94∘
Final Answers
1. Dispersive Power (Ω): Approximately 0.169
2. Angular Dispersion (Δ): Approximately 6.94°
- μR=1.52 (refractive index for red light)
- μV=1.62 (refractive index for violet light)
- μY=1.59 (refractive index for yellow light)
2. Angular Dispersion (Δ): Approximately 6.94°
Similar Questions
The refractive indices of flint glass prism for violet, Yellow and Red colours are 1.790, 1.795 and 1.805 respectively, find dispersive power of the flint glass.
View SolutionThe refractive indices of crown glass prism of C,D and F lines are 1.527, 1.530 and 1.535 respectively. Find the dispersive power of the crown glass prism.
View SolutionThe focal lengths of a convex lens for red, yellow and violet rays are 100 cm, 98 cm and 96 cm respectively. Find the dispersive power of the material of the lens.
View SolutionThe focal lengths of a thin lens for red and violet light are 90.0 cm and 86.4cm respectively. Find the dispersive power of the material of the lens. Make appropriate assumptions.
View SolutionThe refractive indices of violet and red light are 1.54 and 1.52 respectively. If the angle of prism is 10∘, then the angular dispersion is
View SolutionThe deviation produced for violet, yellow and red lights for crown glass are 3.75∘,3.25∘and2.86∘ respectively. Calculate the dispersive power of the crown glass
View SolutionThe refractive indices of the material of the prism and liquid are 1.56 and 1.32 respectively. What will be the value of θ for the following refraction?
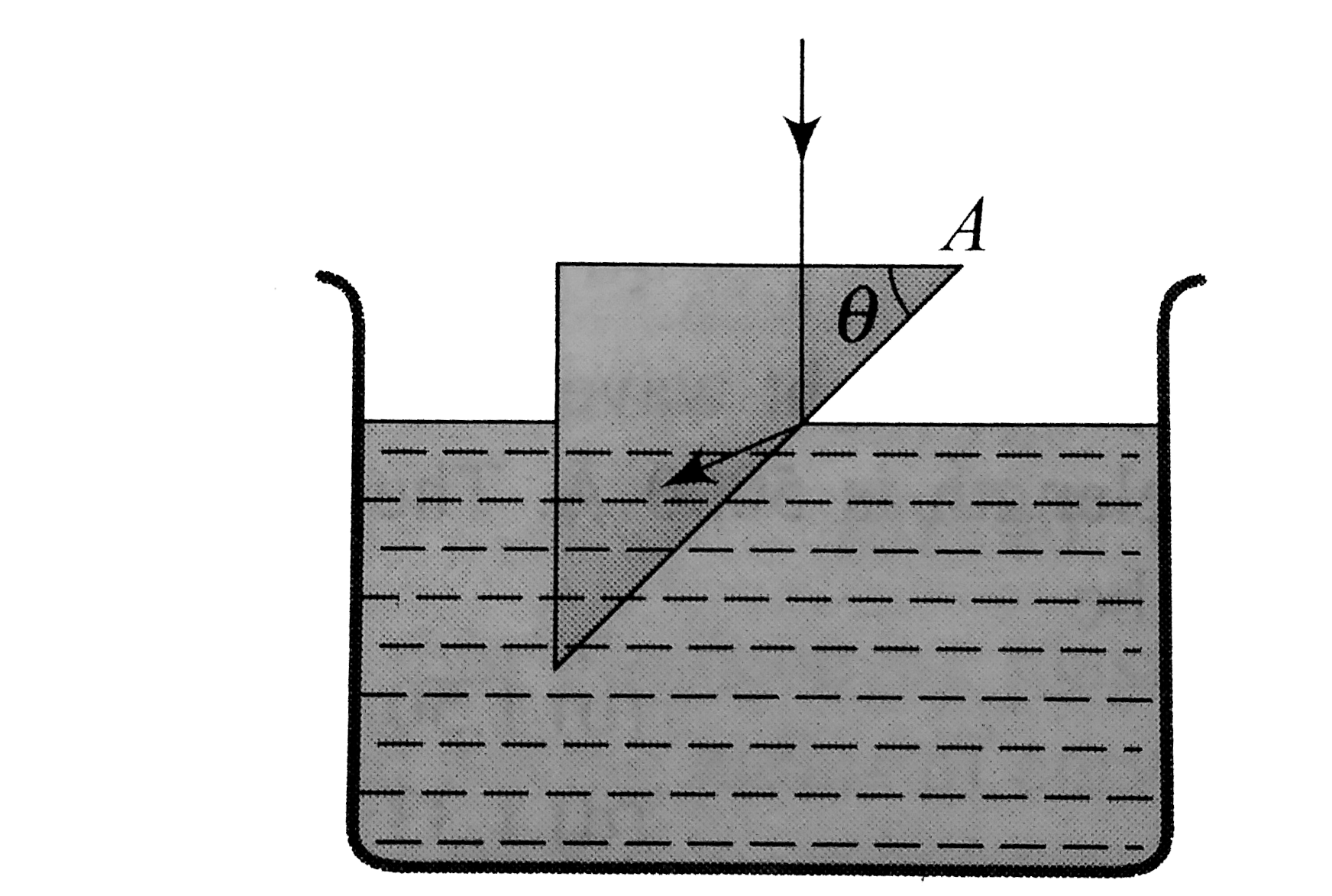
View SolutionThe refractive index of a particular material is 1.67 for blue light, 1.65 for yellow light and 1.63 for red light. The dispersive power of the material is .........
View SolutionThe refractive indicates of flint glass for red and violent colours are 1.644and1.664. Calculate its dispersive power.
View SolutionThe refractive indices of flint glass for red and violet light are 1.613 and 1.632, respectively. Find the angular dispersion produced by the thin prism of flint glass having refracting angle 4∘.
View Solution
