Write two properties of equipotential surfaces.
Step-by-Step Solution:
1. Definition of Equipotential Surface:
An equipotential surface is defined as a surface where all points on that surface have the same electric potential. This means that no work is required to move a charge along the surface since the potential difference is zero.
2. First Property:
The first property of equipotential surfaces is that they are always perpendicular to electric field lines. This means that if you have an electric field created by a charge, the equipotential surfaces will intersect the electric field lines at right angles. For example, if you have a point charge, the equipotential surfaces around it will be spherical, and the electric field lines will radiate outward from the charge, intersecting the equipotential surfaces perpendicularly.
3. Second Property:
The second property is that equipotential surfaces never intersect or cross each other. If two equipotential surfaces were to intersect, it would imply that at the point of intersection, there are two different potentials, which is not possible. Therefore, equipotential surfaces are distinct and do not overlap.
Summary of Properties:
- Property 1: Equipotential surfaces are always perpendicular to electric field lines.
- Property 2: Equipotential surfaces never intersect or cross each other.
---
An equipotential surface is defined as a surface where all points on that surface have the same electric potential. This means that no work is required to move a charge along the surface since the potential difference is zero.
The first property of equipotential surfaces is that they are always perpendicular to electric field lines. This means that if you have an electric field created by a charge, the equipotential surfaces will intersect the electric field lines at right angles. For example, if you have a point charge, the equipotential surfaces around it will be spherical, and the electric field lines will radiate outward from the charge, intersecting the equipotential surfaces perpendicularly.
The second property is that equipotential surfaces never intersect or cross each other. If two equipotential surfaces were to intersect, it would imply that at the point of intersection, there are two different potentials, which is not possible. Therefore, equipotential surfaces are distinct and do not overlap.
- Property 1: Equipotential surfaces are always perpendicular to electric field lines.
- Property 2: Equipotential surfaces never intersect or cross each other.
Similar Questions
Which of the following is NOT the property of equipotential surface? (i) They do not cross each other. (ii) The rate of change of potential with distance on them is zero. (iii) For a uniform electric field they are concentric spheres. (iv) They can be imaginary spheres.
View SolutionWhich of the following is NOT the property of equipotential surface? (i) They do not cross each other. (ii) The rate of change of potential with distance on them is zero. (iii) For a uniform electric field they are concentric spheres. (iv) They can be imaginary spheres.
View SolutionAssertion : Lines of force are perpendicular to conductor surface.
Reason : Generally electric field is perpendicular to equipotential surface.
View SolutionWrite two properties of a material suitable for making (a) a perment magnet,
View SolutionFigure shows a set of equipotential surfaces. The magnitude and direction of electric field that exists in the region is-
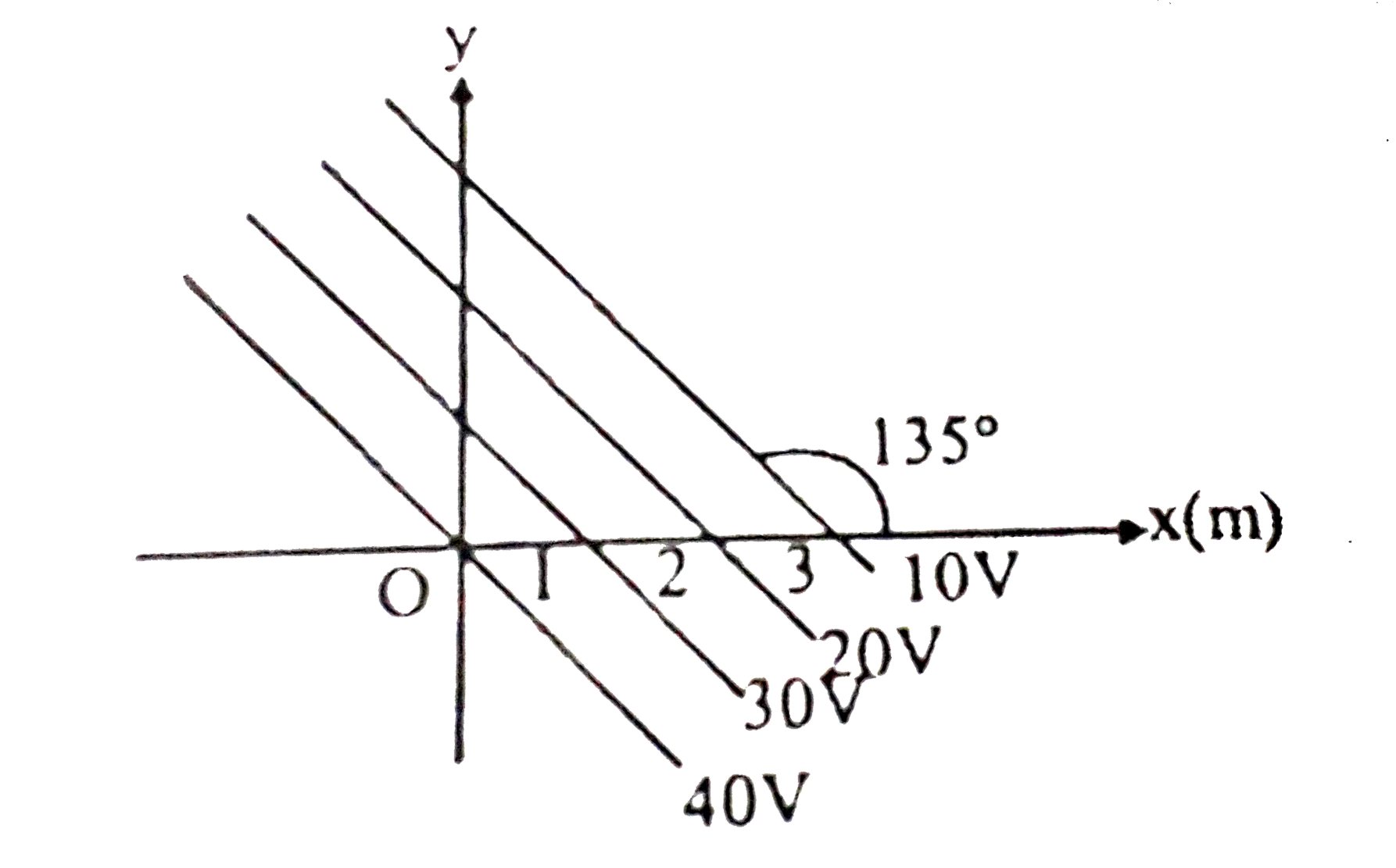
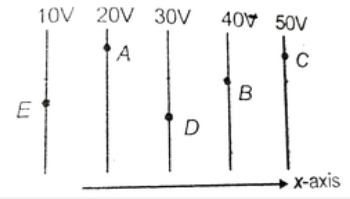
View SolutionFigure shows a set of equipotential surfaces. There are a few points marked on them. An electron is being moved from one point to other. Which of the following statements is / are correct ?
View SolutionWhat is the geometrical shape of equipotential surfaces due to a single isolated charge ?
View SolutionWrite two properties of alkali metals salts of oxo-acids.
View SolutionWrite two properties of alkali metals salts of oxo-acids.
View SolutionAn infinite nonconducting sheet of charge has a surface charge density of 107C/m2. The separation between two equipotential surfaces near the whose potential differ by 5V is
View Solution