Calculate the area covered per second (m2s−1) by the Moon for one complete revolution round the Earth (distance of Moon from Earth =3.845×108 and period of revolution of Moon =2713 days).
To solve the problem of calculating the area covered per second by the Moon during its revolution around the Earth, we will follow these steps:
Step 1: Convert the period of revolution from days to seconds
The period of revolution of the Moon is given as 2713 days. We can convert this to seconds.
T=2713 days=823 days
Now, we convert days to seconds:
T=823 days×24 hours/day×60 minutes/hour×60 seconds/minute
Calculating this gives:
T=823×24×60×60=2361600 seconds
Step 2: Use Kepler's law to find the areal velocity
According to Kepler's law, the areal velocity (area swept per unit time) can be expressed as:
dAdt=R2⋅ω
Where R is the distance from the Earth to the Moon, and ω is the angular velocity. We can relate angular velocity to the period T using:
ω=2πT
Step 3: Substitute ω into the areal velocity formula
Substituting ω into the areal velocity formula gives:
dAdt=R2⋅2πT
Step 4: Substitute the known values
We know:
- R=3.845×108 m
- T=2361600 seconds
Now substituting these values into the formula:
dAdt=(3.845×108)2⋅2π2361600
Step 5: Calculate the area covered per second
Calculating R2:
R2=(3.845×108)2=1.477×1017 m2
Now substituting this back into the equation:
dAdt=1.477×1017⋅2π2361600
Calculating the numerical value:
dAdt≈1.97×1011 m2/s
Final Result
Thus, the area covered per second by the Moon during its revolution around the Earth is approximately:
dAdt≈1.97×1011 m2/s
---
The period of revolution of the Moon is given as 2713 days. We can convert this to seconds.
According to Kepler's law, the areal velocity (area swept per unit time) can be expressed as:
Substituting ω into the areal velocity formula gives:
We know:
- R=3.845×108 m
- T=2361600 seconds
Calculating R2:
Thus, the area covered per second by the Moon during its revolution around the Earth is approximately:
Topper's Solved these Questions
- SAMPLE QUESTION PAPER - 01 Book:ICSEChapter:SAMPLE QUESTION PAPER - 01 Exercise:SECTION - C
Explore 14 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
Explore 12 Videos
- SAMPLE QUESTION PAPER 4Book:ICSEChapter:SAMPLE QUESTION PAPER 4Exercise:SECTION - D (Answer all questions.)
Explore 7 Videos
Similar Questions
You are given the following data :g=9.81ms−2, radius of earth =6.37×106m the distance of the Moon from the earth =3.84×108m and the time period of the Moon's revolution =27.3days. Obtain the mass of the earth in two different ways. G=6.67×10−11Nm2kg−2.
View SolutionYou are given the following data :g=9.81ms−2, radius of earth =6.37×106m the distance the Moon from the earth =3.84×108m and the time period of the Moon's revolution =27.3days. Obtain the mass of the earth in two different ways. G=6.67×10−11Nm2kg2.
View SolutionGiven that T2=kR3, express the constant k of the above relation in days and kilometres. Given, k=10−13s2m−3. The Moon is at a distance of 3.84×105km from the earth. Obtain its time period of revolution in days.
View SolutionGiven that T2=kR3, express the constant k of the above relation in days and kilometres. Given, k=10−13s2m−3. The Moon is at a distance of 3.84×105km from the earth. Obtain its time period of revolution in days.
View SolutionGiven that T2=kR3, express the constant k of the above relation in days and kilometres. Given, k=10−13s2m3. The Moon is at a distance of 3.84×105km from the earth. Obtain its time period of revolution in days.
View SolutionA bomb explodes on moon. How long does the sound take to reach the earth (average distance between the earth and moon 3.8×108m)
View SolutionThe distance of the planet Jupiter from the Sun is 5.2 times that of the Earth. Find the period of Jupiter's revolution around the Sun.
View SolutionCalculate the distance from the earth to the point where the gravitational field due to the earth and the moon cancel out. Given that the earth-moon distance is 3.8×108m and the mass of earth is 81 times that of moon.
View SolutionThe Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
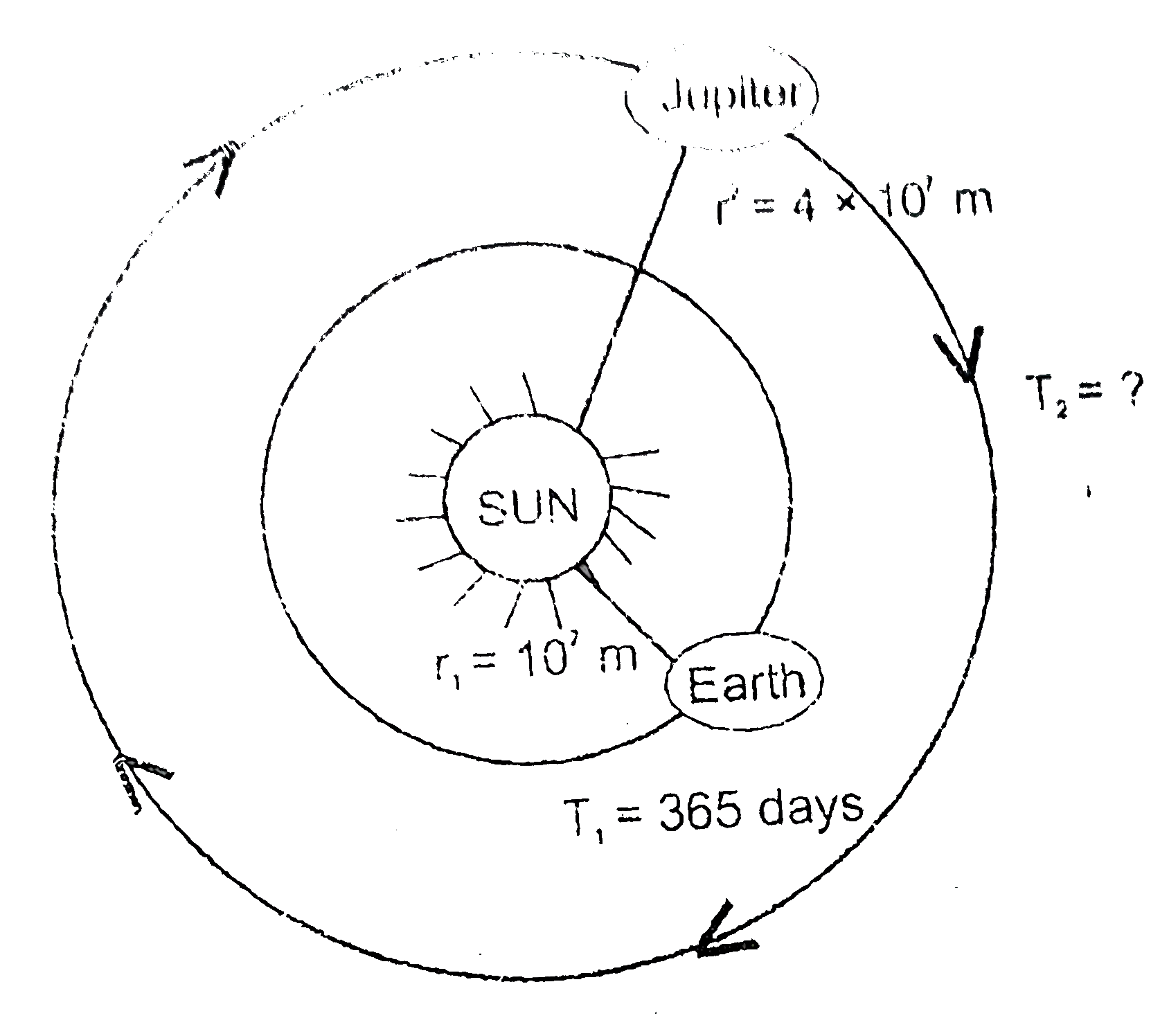 .
.
View SolutionCompare the distance of the sun from the earth and the distance of the mars from the Earth if the Sun is 1.5×108 km from the Earth and the Mars is 5.5×107 km from the Earth.
View Solution