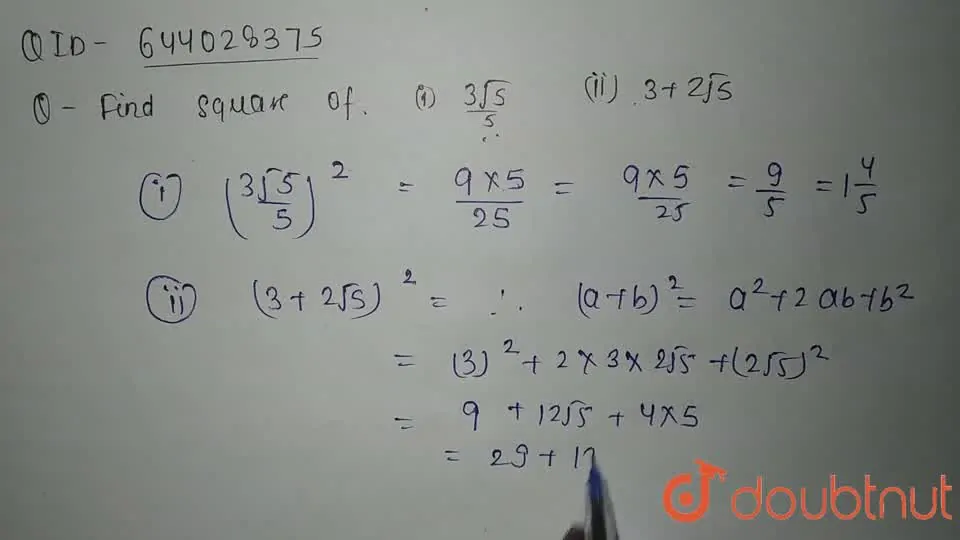Find the square of :
(i) 3√55 (ii) 3+2√5
The correct Answer is:(i) 145 (ii) 29+12√5
Step by step video, text & image solution for Find the square of : (i) (3sqrt(5))/5" (ii) "3+2sqrt(5) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Similar Questions
Find the square of :
3√55View SolutionFind the square of :
3+2√5View SolutionFind the square of :
√5−2View SolutionRationalize the denominator of :
(i) 2√3√5 (ii) 1√3−√2View SolutionFind the value of √5 correct to 2 decimal places, then use it to find the square root of 3−√53+√5 correct to 2 significant digits.
View SolutionFind duplicate ratio of:
(i) 3:4
(ii) 3√3:2√5View SolutionRationalise the denominator of each of the following
(i)3√5
(ii) 32√5View SolutionRationalize the denominatior and simplify to find the value of 4√5+√3
(Given : √5=2.236and√3 = 1.732)View SolutionWrite the lowest rationalising factor of :
(i) 5√2 (ii) √18−√50 (iii) (2√2+2√3)View SolutionFind the value of a and b if
(i)√3+1√3−1=a+b√3 (ii)5+2√35−2√3=a+b√3View Solution