Question

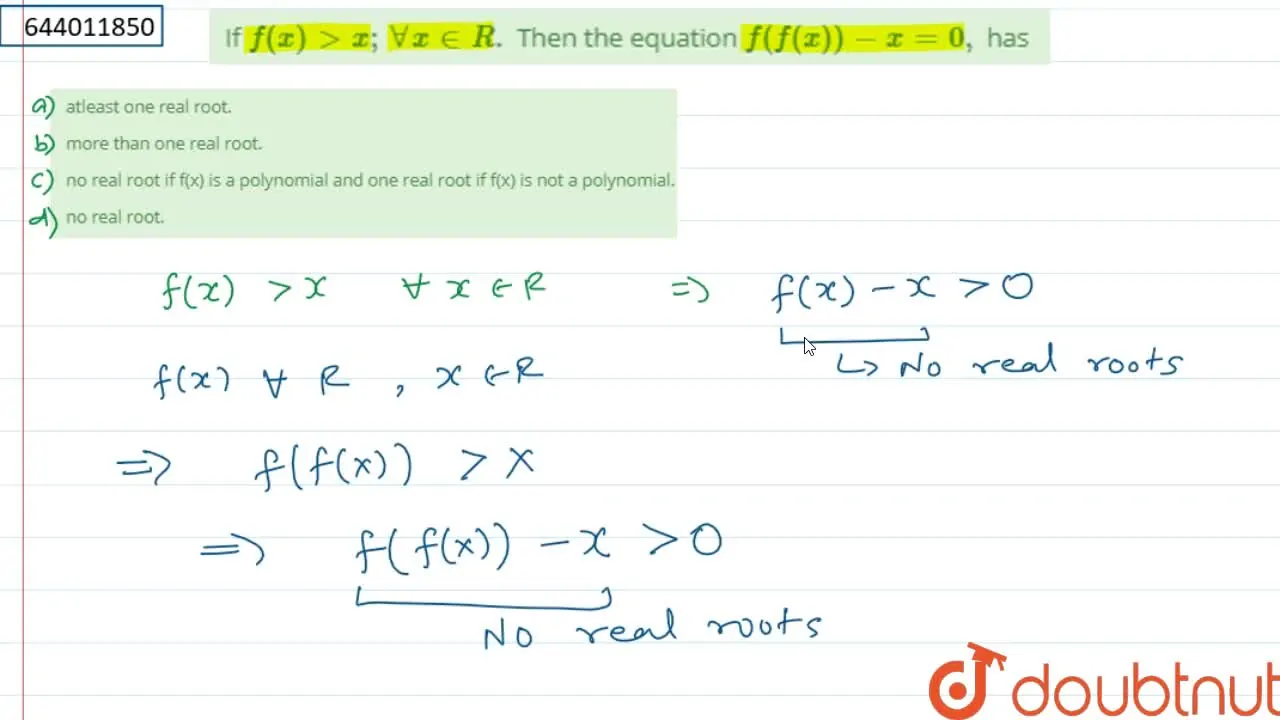
If ${\displaystyle f\left(x\right)>x;\forall x\in R.}$ Then the equation ${\displaystyle f\left(f\left(x\right)\right)-x=0,}$ has

Options

A. atleast one real root.
B. more than one real root.
C. no real root if f(x) is a polynomial and one real root if f(x) is not a polynomial.
D. no real root.

Answer

D

Explanation

To solve the problem, we need to analyze the given condition and the equation step by step.

1. Understanding the Given Condition:
We are given that \( f(x) > x \) for all \( x \in \mathbb{R} \). This means that the function \( f(x) \) is always above the line \( y = x \) for every real number \( x \).

Hint: Consider what it means for a function to be greater than the identity function.

2. Rearranging the Equation:
We need to analyze the equation \( f(f(x)) - x = 0 \). Rearranging gives us:
\( f(f(x)) = x \)
This means we are looking for values of \( x \) such that applying \( f \) twice returns \( x \).

Hint: Think about the implications of applying \( f \) twice and how it relates to the original condition.

3. Applying the Condition:
Since \( f(x) > x \), applying \( f \) to both sides gives:
\( f(f(x)) > f(x) > x \)
This shows that \( f(f(x)) \) is also greater than \( x \).

Hint: Use the transitive property of inequalities to relate \( f(f(x)) \) and \( x \).

4. Conclusion About Roots:
From the inequality \( f(f(x)) > x \), we can conclude that \( f(f(x)) - x > 0 \) for all \( x \in \mathbb{R} \). This means that the left-hand side of our equation \( f(f(x)) - x = 0 \) is always positive and thus can never be zero.

Hint: Consider the implications of a function that is always positive in relation to finding roots.

5. Final Answer:
Since \( f(f(x)) - x \) is always greater than zero, the equation \( f(f(x)) - x = 0 \) has no real roots.

Therefore, the final answer is that the equation has no real roots.

Summary of the Steps:
1. Analyze the condition \( f(x) > x \).
2. Rearrange the equation to \( f(f(x)) = x \).
3. Use the condition to show \( f(f(x)) > x \).
4. Conclude that \( f(f(x)) - x > 0 \) implies no roots.
5. State the final conclusion.