If f(x)=3(2x+3)2/3+2x+3, then:
(a) f(x) is continuous but not differentiable at x=−32
(b) f(x) is differentiable at x=0
(c) f(x) is continuous at x=0
(d) f(x) is differentiable but not continuous at x=−32
The correct Answer is:A, B, C
To solve the problem, we need to analyze the function f(x)=3(2x+3)23+2x+3 for its continuity and differentiability at the points x=0 and x=−32.
Step 1: Check Continuity at x=0
To check continuity at x=0, we need to find f(0) and ensure that the limit as x approaches 0 equals f(0).
1. Calculate f(0):
f(0)=3(2(0)+3)23+2(0)+3=3(3)23+3=3⋅323+3
Since 323=√(3)9, we can simplify:
f(0)=3⋅√(3)9+3
2. Calculate the limit as x approaches 0:
limx→0f(x)=limx→0(3(2x+3)23+2x+3)
Substitute x=0:
=3(3)23+3=3⋅√(3)9+3
Thus, limx→0f(x)=f(0).
Since both the limit and the function value at x=0 are equal, f is continuous at x=0.
Step 2: Check Differentiability at x=0
To check differentiability at x=0, we need to find f′(x).
1. Differentiate f(x):
f′(x)=3⋅23(2x+3)−13⋅2+2
Simplifying this:
f′(x)=2(2x+3)−13⋅2+2=4(2x+3)13+2
2. Evaluate f′(0):
f′(0)=4(2(0)+3)13+2=4313+2
This is defined, so f is differentiable at x=0.
Step 3: Check Continuity and Differentiability at x=−32
1. Calculate f(−32):
f(−32)=3(2(−32)+3)23+2(−32)+3=3(0)23−3+3=0
2. Check the limit as x approaches −32:
limx→−32f(x)=f(−32)=0
Thus, f is continuous at x=−32.
3. Check differentiability at x=−32:
f′(−32)=4(2(−32)+3)13+2=4013+2
This is undefined, so f is not differentiable at x=−32.
Conclusion
- f is continuous at x=0 and differentiable at x=0.
- f is continuous at x=−32 but not differentiable.
Final Answers:
- a) True: f is continuous but not differentiable at −32.
- b) True: f is differentiable at 0.
- c) True: f is continuous at 0.
- d) False: f is not differentiable but continuous at −32.
f(0)=3(2(0)+3)23+2(0)+3=3(3)23+3=3⋅323+3
Since 323=√(3)9, we can simplify:
f(0)=3⋅√(3)9+3
limx→0f(x)=limx→0(3(2x+3)23+2x+3)
Substitute x=0:
=3(3)23+3=3⋅√(3)9+3
Thus, limx→0f(x)=f(0).
f′(x)=3⋅23(2x+3)−13⋅2+2
Simplifying this:
f′(x)=2(2x+3)−13⋅2+2=4(2x+3)13+2
f′(0)=4(2(0)+3)13+2=4313+2
This is defined, so f is differentiable at x=0.
f(−32)=3(2(−32)+3)23+2(−32)+3=3(0)23−3+3=0
limx→−32f(x)=f(−32)=0
Thus, f is continuous at x=−32.
f′(−32)=4(2(−32)+3)13+2=4013+2
This is undefined, so f is not differentiable at x=−32.
- f is continuous at x=−32 but not differentiable.
- a) True: f is continuous but not differentiable at −32.
- b) True: f is differentiable at 0.
- c) True: f is continuous at 0.
- d) False: f is not differentiable but continuous at −32.
Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBook:ARIHANT MATHS ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise (Statement I And Ii Type Questions)
Explore 11 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:ARIHANT MATHS ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:EXERCISE 4
Explore 3 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:ARIHANT MATHS ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise (Single Option Correct Type Questions)
Explore 48 Videos
- COMPLEX NUMBERSBook:ARIHANT MATHS ENGLISHChapter:COMPLEX NUMBERSExercise:Complex Number Exercise 8
Explore 2 Videos
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHS ENGLISHChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 7 Videos
Similar Questions
Knowledge Check
The graph of f(x)=x−3x2−2x−3 is shown below. What is the domain of f(x) ?
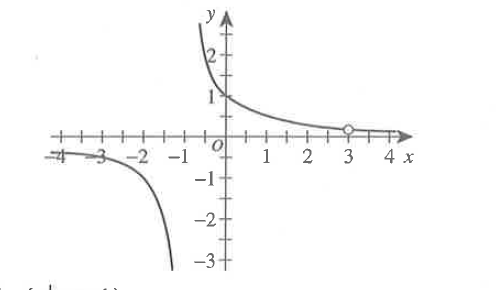 A{x∣x≠−1}B{x∣x≠2}C{x∣x≠3}D{x∣x≠−1andx≠3}
A{x∣x≠−1}B{x∣x≠2}C{x∣x≠3}D{x∣x≠−1andx≠3}If f(x)=2x3 and g(x)=3x, what is the value of g(f(−2))−f(g(−2)) ?
A−480B−384C0D384
Find the derivative of f(x)=2x3+3x2+5x+9 at x = 2
View SolutionIf f(x)=3x2, then f'(2)=
View SolutionThe greatest value of the function f(x)=2.33x−32x.4+2.3x in the interval [−1,1] is
View SolutionIf f(x)=x4+3x2−6x−2 then the coefficient of x3 in f(x+1) is
View SolutionIf f1(x)=2x+3,f2(x)=3x2+5,f3(x)=x+cosx are defined from R→R, then f1,f2 and f3 are
View SolutionIf f(x)=12(3x+3−x),g(x)=12(3x−3−x), then f(x) g(y)+f(y) g(x)=
View Solution

