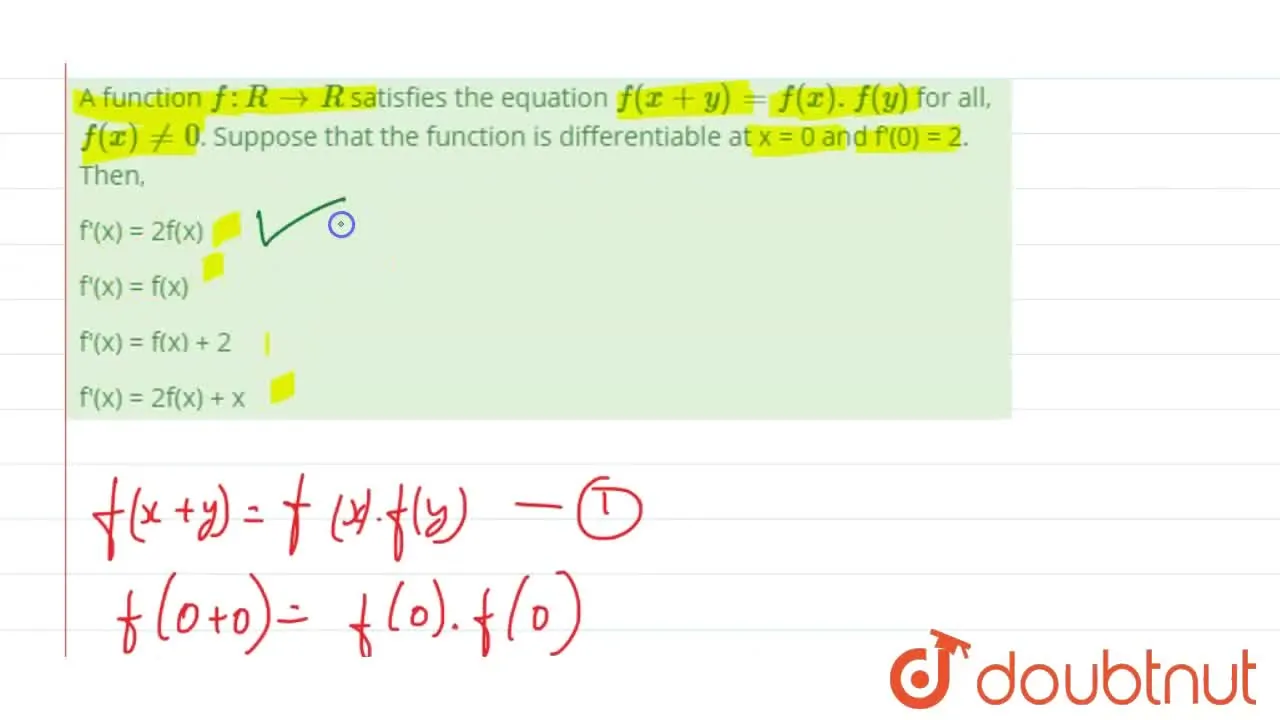
A function f:R→R satisfies the equation f(x+y)=f(x).f(y) for all, f(x)≠0. Suppose that the function is differentiable at x = 0 and f'(0) = 2. Then,
f'(x) = 2f(x)
f'(x) = f(x)
f'(x) = f(x) + 2
f'(x) = 2f(x) + x
The correct Answer is:A
Step by step video & image solution for A function f : R rarr R satisfies the equation f(x + y) = f(x) . f(y) for all, f(x) ne 0. Suppose that the function is differentiable at x = 0 and f'(0) = 2. Then, by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXAMPLE1videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise For Session 15videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 82videos
COMPLEX NUMBERS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
Similar Questions
A function f:R→R satisfies the equation f(x+y)=f(x).f(y) for all xy∈R,f(x)≠0. Suppose that the function is differentiable at x=0 and f'(0)=2, then prove that f'=2f(x).
View SolutionA function f:R→R satisfies that equation f(x+y)=f(x)f(y) for all x, y∈R , f(x)≠0 . Suppose that the function f(x) is differentiable at x=0 and f′(0)=2 . Prove that f′(x)=2 f(x) .
View SolutionA function f:R→R satisfies that equation f(x+y)=f(x)f(y) for all x, y∈R , f(x)≠0 . Suppose that the function f(x) is differentiable at x=0 and f′(0)=2 . Prove that f′(x)=2 f(x) .
View SolutionA function f:R→R satisfy the equation f(x)f(y)−f(xy)=x+y for all x,y∈R and f(y)>0, then
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for allx,y∈R and f(x)≠0 for all x∈R. If f(x) is differentiable at x=0andf′(0)=2, then prove that f′(x)=2f(x).
View SolutionA function f : R→R satisfies the equation f(x)f(y)−f(xy)=x+y∀x,y∈Randf(1)>0, then
View SolutionIf a real valued function f(x) satisfies the equation f(x+y)=f(x)+f(y) for all x,y∈R then f(x) is
View SolutionA function f:R→R satisfies the relation f(x+y3)=13|f(x)+f(y)+f(0)| for all x,y∈R. If f'(0) exists, prove that f'(x) exists for all x,∈R.
View SolutionA function f(x) satisfies the relation f(x+y)=f(x)+f(y)+xy(x+y),∀x,y∈R. If f'(0) = - 1, then
View SolutionA function f:R→R+ satisfies f(x+y)=f(x)f(y)∀x∈R If f'(0)=2 then f'(x)=
View Solution