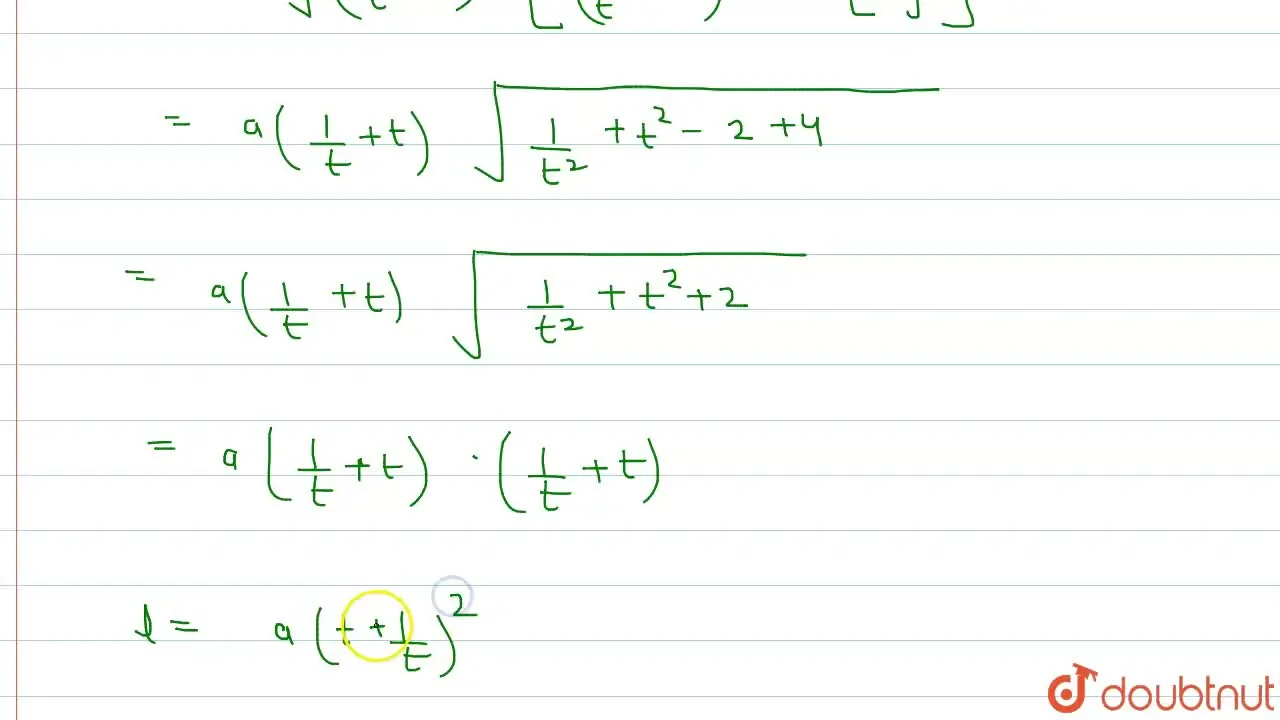If the point () be the extremity of a focal chord of parabola then show that the length of the focal chord is .
The correct Answer is:4a
Step by step video & image solution for If the point (at^2,2at) be the extremity of a focal chord of parabola y^2=4ax then show that the length of the focal chord is a(t+1/t)^2 . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - JEE type solved examples1videos
PARABOLA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise For Session 120videos
PARABOLA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)2videos
PAIR OF STRAIGHT LINES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)28videos
PERMUTATIONS AND COMBINATIONS
Similar Questions
If b and k are segments of a focal chord of the parabola y2=4ax, then k =
View SolutionIf (2,−8) is at an end of a focal chord of the parabola y2=32x, then find the other end of the chord.
View SolutionIf (2,−8) is at an end of a focal chord of the parabola y2=32x, then find the other end of the chord.
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf the point P(4, -2) is the one end of the focal chord PQ of the parabola y2=x, then the slope of the tangent at Q, is
View SolutionLength of the shortest normal chord of the parabola y2=4ax is
View SolutionOne end point of a focal chrod of a parabola y2=16x is (1,4). The length of focal chord is : (A)24 (B)25 (C)20 (D)=22
View SolutionFind the locus of the midpoint of normal chord of parabola y2=4ax
View Solution