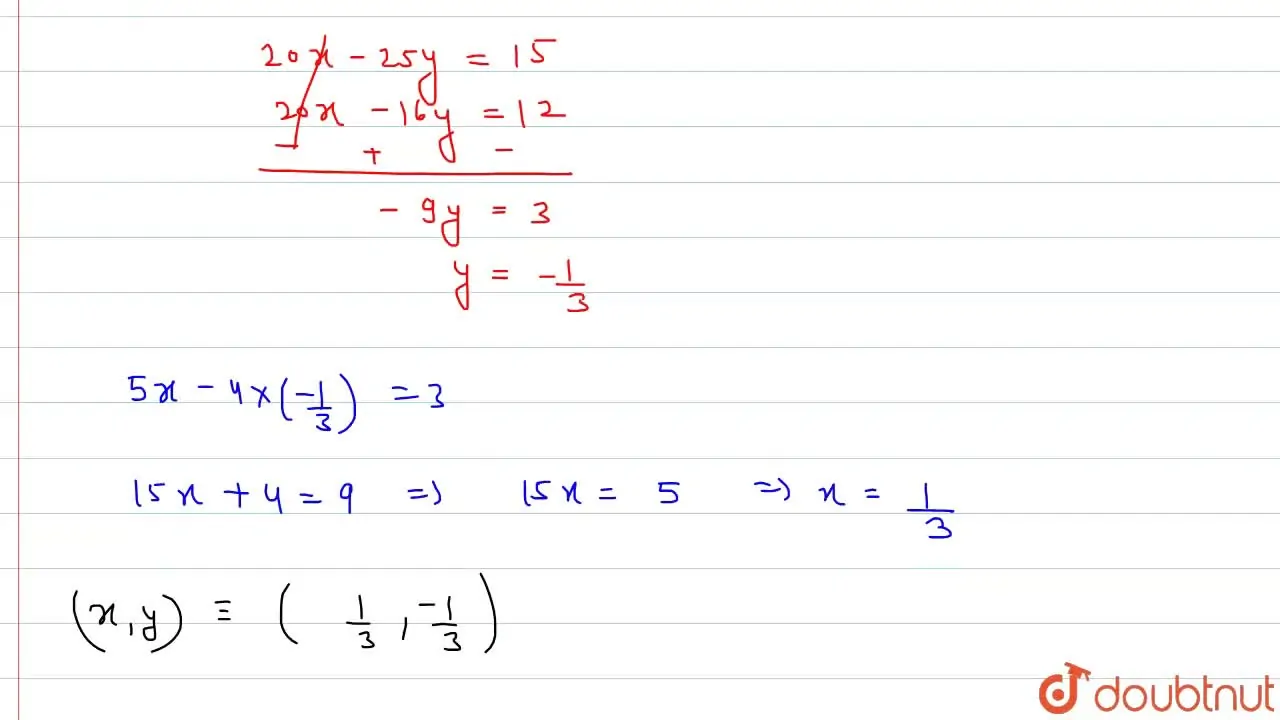The point of intersection of the two lines given by 2x2−5xy+2y2−3x+3y+1=0 is
A. (-2,2)
B. (-3,3)
C. (3,3)
D. (2,2)
The correct Answer is:C
Step by step video & image solution for The point of intersection of the two lines given by 2x^2-5xy +2y^2-3x+3y+1=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (More Than One Correct Option Type Questions)6videos
PAIR OF STRAIGHT LINES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Passage Based Questions)9videos
PAIR OF STRAIGHT LINES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise For Session 510videos
PAIR OF STRAIGHT LINES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)29videos
MONOTONICITY MAXIMA AND MINIMA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)36videos
PARABOLA
Similar Questions
The point of intersection of the pair of straight lines given by 6x2+5xy−4y2+7x+13y−2=0, is
View SolutionThe equation of the line joining the origin to the point of intersection of the lines 2x2+xy−y2+5x−y+2=0 is
View SolutionFind the point of intersection of the lines 2x−3y+8=0 and 4x+5y=6
View SolutionFind the co-ordinates of the point of intersection of the straight lines
2x−3y−7=0,3x−4y−13=0View SolutionFind the co-ordinates of the point of intersection of the straight lines
3x−5y+5=0,2x+3y−22=0View SolutionThe four point of intersection of the lines (2x−y+1)(x−2y+3)=0 with the axes lie on a circle whose center centre is at the point :
View SolutionEquation of the tangent to the circle at the point (1, -1) whose centre is the point of intersection of the straight lines x-y=1 and 2x+y-3=0, is
View SolutionFind the point of intersection of the lines 4x+3y=1 and 3x−y+9=0. If this point lies on the line (2k−1)x−2y=4, find the value of k.
The above question can also be stated as : If the lines 4x+3y=1,3x–y+9=0 and (2k−1)x−2y=4 are concurrent (pass through the same point), find the value of k.View SolutionIf the pairs of lines x2+2xy+ay2=0 and ax2+2xy+y2=0 have exactly one line in common, then the joint equation of the other two lines is given by 3x2+8xy−3y2=0 3x2+10xy+3y2=0 y2+2xy−3x2=0 x2+2xy−3y2=0
View SolutionShow that the four points of intersection of the lines : (2x−y+1) (x-2y+3) = 0, with the axes lie on a circle and find its centre.
View Solution