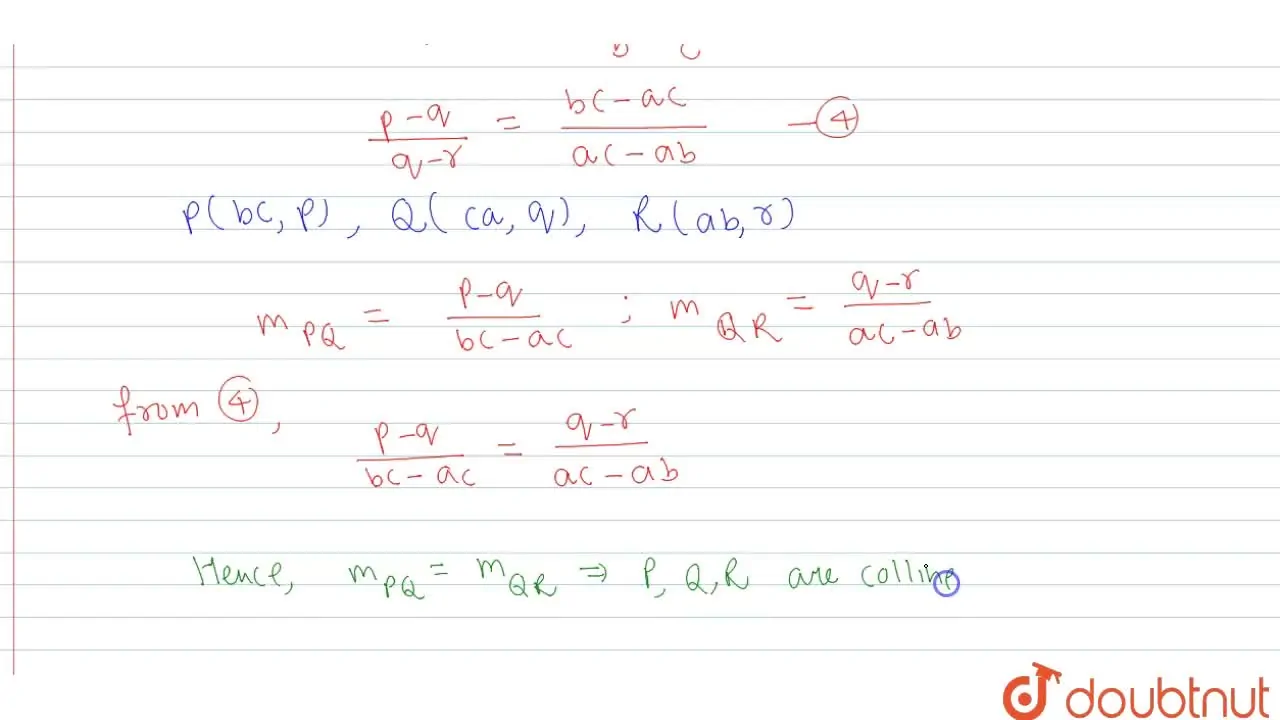If a, b, c be the pth, qth and rth terms respectively of a HP, show that the points (bc, p), (ca, q) and (ab, r) are collinear.
Step by step video & image solution for If a, b, c be the pth, qth and rth terms respectively of a HP, show that the points (bc, p), (ca, q) and (ab, r) are collinear. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - EXERCISE : 74videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)20videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
DEFINITE INTEGRAL
Similar Questions
If a,b,c are the pth,qth,rth terms, respectively, of an HP , show that the points (bc,p),(ca,q), and (ab,r) are collinear.
View SolutionIf a,b,c are the pth,qth,rth terms, respectively, of an HP , show that the points (bc,p),(ca,q), and (ab,r) are collinear.
View SolutionIf a,b,c are the pth,qth,rth terms respectively of an H.P., then the lines bcx+py+1=0,cax+qy+1=0andabx+ry+1=0 (A) are concurrent (B) form a triangle (C) are parallel (D) none of these
View SolutionIf a,b,c be the pth, qth and rth terms respectively of a H.P., the ∣∣ ∣ ∣∣bcp1caq1abr1∣∣ ∣ ∣∣= (A) 0 (B) 1 (C) -1 (D) none of these
View SolutionIf a,b,c, be the pth, qth and rth terms respectivley of a G.P., then the equation aqbrcpx2+pqrx+arb−pcq=0 has (A) both roots zero (B) at least one root zero (C) no root zero (D) both roots unilty
View SolutionIf a,b,c are positive and are the pth,qthrth terms respectively of a GP then ∣∣ ∣ ∣∣logap1logbq1logcr1∣∣ ∣ ∣∣=
View SolutionIf rational numbers a,b,c be th pth, qth, rth terms respectively of an A.P. then roots of the equation a(q−r)x2+b(r−p)x+c(p−q)=0 are necessarily (A) imaginary (B) rational (C) irrational (D) real and equal
View SolutionIf pth, qth and rth terms of a HP be respectivelya,b and c, has prove that (q−r)bc+(r−p)ca+(p−q)ab=0.
View SolutionIf a , b and c b respectively the pth , qth and rth terms of an A.P. prove that
a(q-r) +b(r-p) +c (p-q) =0View SolutionIf a, b,c are the pth, qth, and rth terms of a HP, then the vectors →u=ˆia+ˆjb+ˆkcand→v=(q−r)ˆi+(r−p)ˆj+(p−q)ˆk
View Solution