Find the polar coordinates of the points whose cartesian coordinates are
(−2,−2)
The correct Answer is:(2,2)≠(−2,−2)
Step by step video & image solution for Find the polar coordinates of the points whose cartesian coordinates are (-2, -2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 110videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 219videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)20videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
DEFINITE INTEGRAL
Similar Questions
Find the polar coordinates of the points whose cartesian coordinates are
(−3,4)View SolutionThe polar coordinates of the point whose cartesian coordinates are (-1, -1) is
View SolutionFind the cartesian coordinates of the points whose polar coordinates are
(5,π−tan−1(43))View SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionThe cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is
View SolutionConvert the polar coordinates to its equivalent Cartesian coordinates(2,π).
View SolutionConvert the following points from polar coordinates to the corresponding Cartesian coordinates.
(i) (2,π/3)
(ii) (0.π/2)
(iii) (−√2,π/4)View SolutionThe cartesian coordinates of the point Q in the figure is
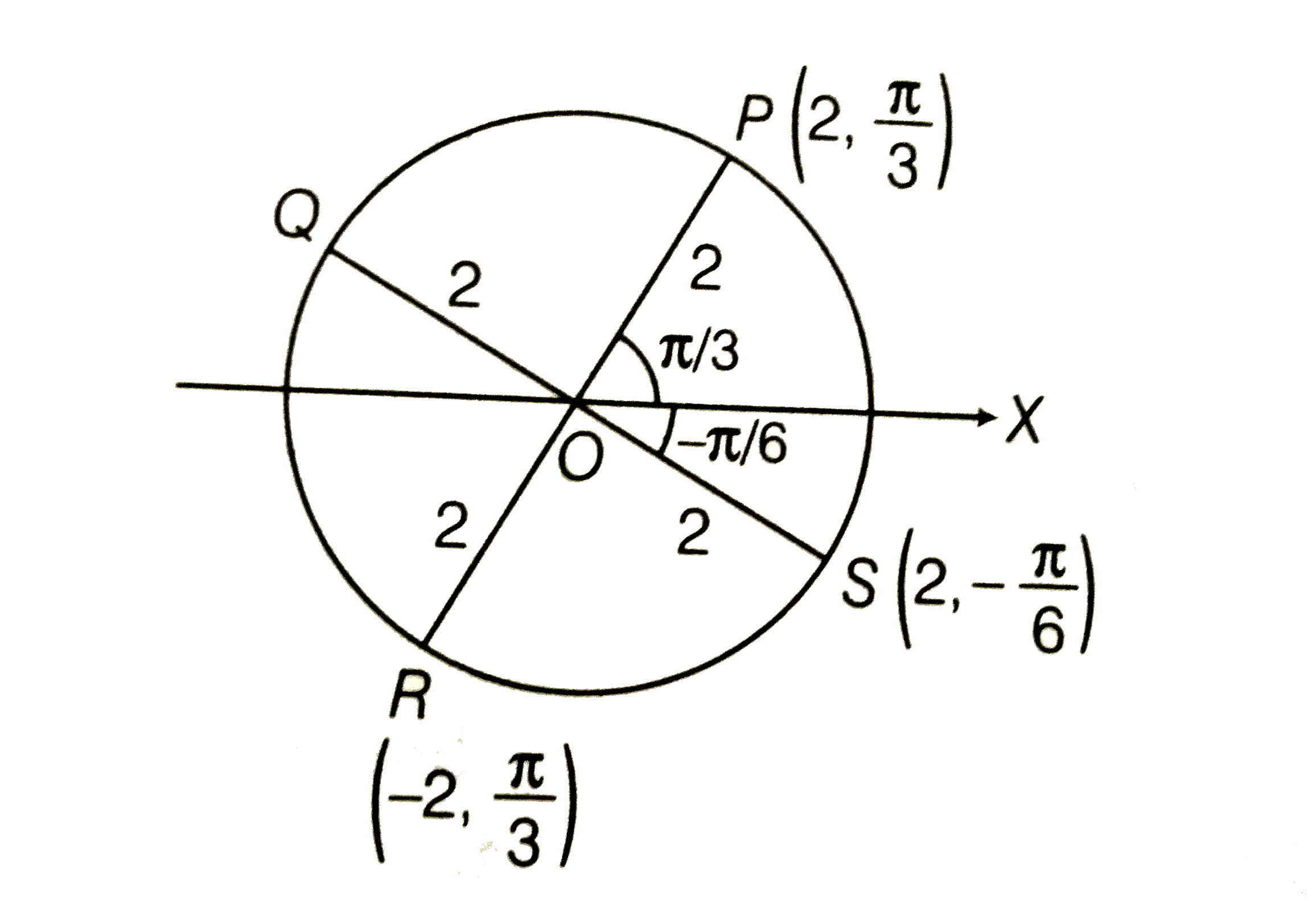 View Solution
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionFind the equation of the circle, the coordinates of the end points of whose diameter are (−1,2)and(4,−3).
View Solution


