If A=[klmn] and kn≠lm, show that A2−(k+n)A+(kn−lm)l=O. Hence, find A−1
To solve the problem, we need to show that A2−(k+n)A+(kn−lm)I=O and then find the inverse of matrix A.
Step 1: Calculate A2
Given the matrix A=(klmn), we can calculate A2 as follows:
A2=A⋅A=(klmn)⋅(klmn)
Calculating the product:
A2=(k2+lmkl+lnmk+nmml+n2)
Step 2: Calculate (k+n)A
Next, we compute (k+n)A:
(k+n)A=(k+n)(klmn)=((k+n)k(k+n)l(k+n)m(k+n)n)
Step 3: Calculate (kn−lm)I
Now, we compute (kn−lm)I, where I is the identity matrix:
(kn−lm)I=(kn−lm)(1001)=(kn−lm00kn−lm)
Step 4: Substitute into the equation
Now we substitute A2, (k+n)A, and (kn−lm)I into the equation:
A2−(k+n)A+(kn−lm)I=(k2+lmkl+lnmk+nmml+n2)−((k+n)k(k+n)l(k+n)m(k+n)n)+(kn−lm00kn−lm)
Step 5: Combine the matrices
Now, we combine the matrices:
1. For the first element:
k2+lm−(k2+nk)+(kn−lm)=0
2. For the second element:
kl+ln−((k+n)l)+0=0
3. For the third element:
mk+nm−((k+n)m)+0=0
4. For the fourth element:
ml+n2−((k+n)n)+(kn−lm)=0
Since all the elements equal zero, we conclude that:
A2−(k+n)A+(kn−lm)I=O
Step 6: Find A−1
To find the inverse of A, we first calculate the determinant of A:
det(A)=kn−lm
Since kn≠lm (as given), det(A)≠0, and thus A−1 exists. The formula for the inverse of a 2x2 matrix is:
A−1=1det(A)(d−b−ca)
Where A=(abcd).
Substituting a=k,b=l,c=m,d=n:
A−1=1kn−lm(n−l−mk)
Final Answer
Thus, we have shown that A2−(k+n)A+(kn−lm)I=O and found the inverse:
A−1=1kn−lm(n−l−mk)
k2+lm−(k2+nk)+(kn−lm)=0
kl+ln−((k+n)l)+0=0
mk+nm−((k+n)m)+0=0
ml+n2−((k+n)n)+(kn−lm)=0
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise For Session 19videos
MATRICES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise For Session 219videos
MATRICES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)2videos
MATHEMATICAL INDUCTION
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)29videos
MONOTONICITY MAXIMA AND MINIMA
Similar Questions
If a=xm+n yl, b=xn+l ym and c=xl+myn, prove that am−n bn−l cl−m =1
View SolutionIf a=xm+n.Yl,b=xn+l.Ymandc=xl+m.Yn,
Prove that : am−n.bn−1.cl−m=1View SolutionIf n and k are positive integers, show that 2k(.nC0)(.nCk)−2k−1(.nC1)(.n−1Ck−1)+2k−2(.nC2)((n−2k−2)).−...+(−1)k(^nCk)+(.n−kC0)=(.nCk)where(.nCk) stands for .nCk.
View SolutionIf L={1,2,3,4},M={3,4,5,6} and N={1,3,5}, then verify that L−(M∪N)=(L−M)∩(L−N).
View SolutionShow that ⌊kn is divisible by (⌊n)k
View SolutionIf y=e−xcosx and yn+kny=0 where yn=dnydxn and kn are constant n∈N then
View SolutionIf y=e−xcosx and yn+kny=0 where yn=dnydxn and kn are constant n∈N then
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
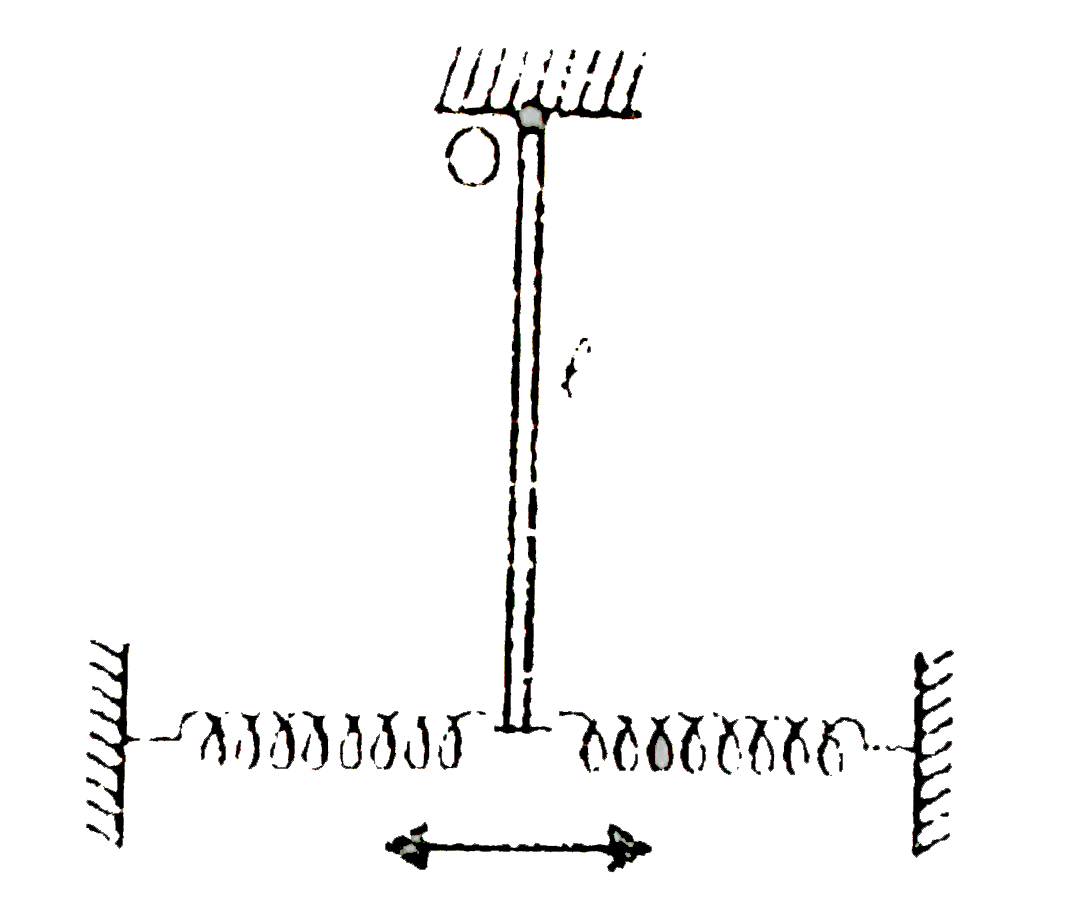 View Solution
View Solution
If the direction cosines of two lines are (l1,m1,n1) and
(l2,m2,n2) and the angle between them is θ then
l21+m21+n21=1=l22+m22+n22
and costheta=l1l2+m1m2+n1n2
If the angle between the lines is 60∘ then the value
of l1(l1+l2)+m1(m1+m2)+n1(n1+n2) isView SolutionIf ln=∫π40tannxdx show that 1l2+l4,1l3+l5,1l4+l6,1l5+l7,.... from an AP. Find its common difference.
View Solution
