If D, E and F are three points on the sides BC, CA and AB, respectively, of a triangle ABC such that the lines AD, BE and CF are concurrent, then show that
BDCD⋅CEAE⋅AFBF=−1
Here, D, E and F be the points on the sides BC,CA and AB respectively of ΔABC. Such that points D,E and F are collinear, be shawn as the adjoining figuece.
Let B as the origin, BA=a and BC=c
The, BF=ka and BD=lc
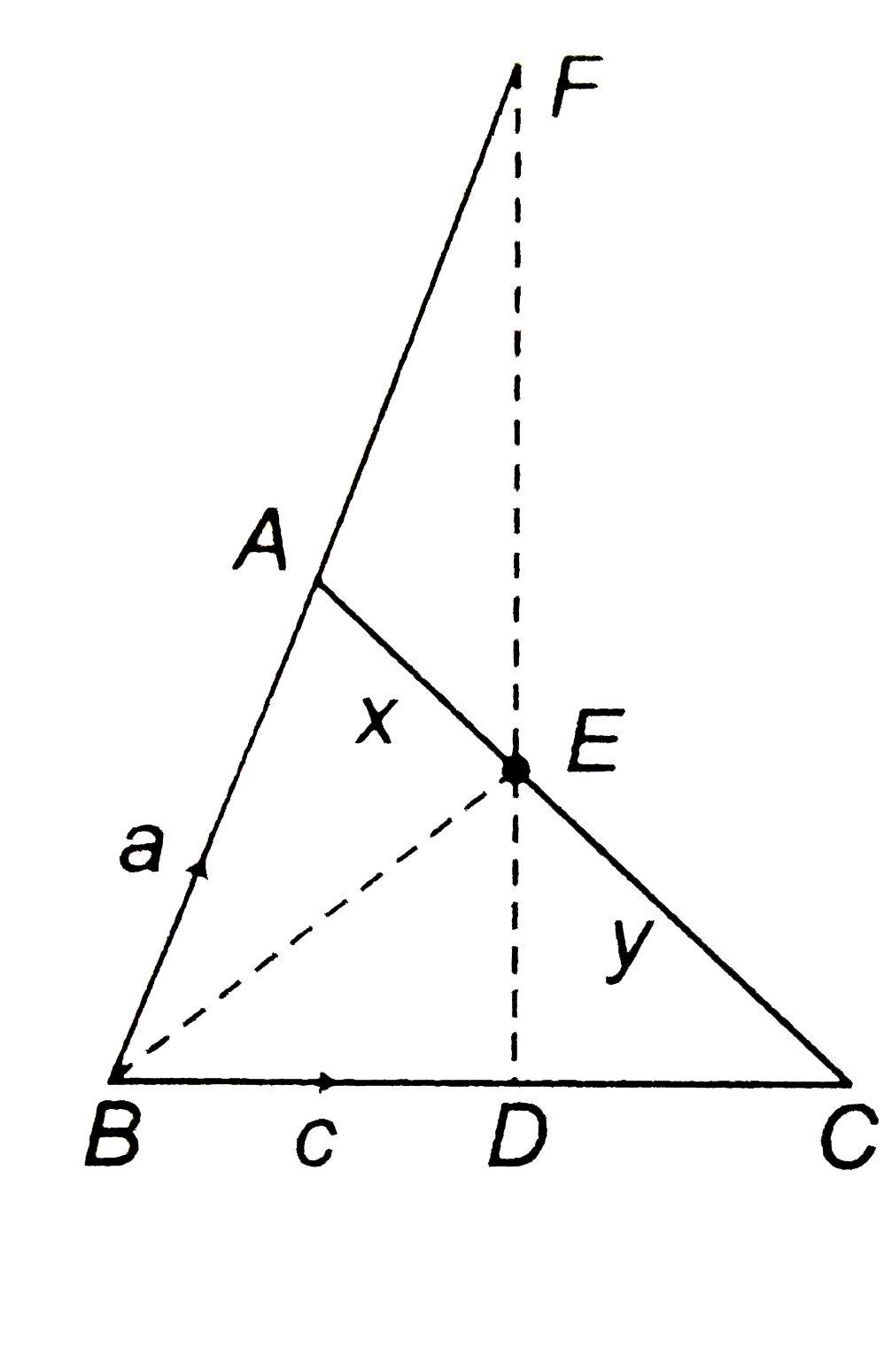
where, k and l are scalars.
∴BDBC=landBFBA=k
⇒BC:BD=1:l
⇒BCBD−1=1l−1⇒DCBD=1−ll
⇒BDDC=l1−landBABF=1k
⇒1−BABF=1−1k⇒AFBF=k−1k
Now, let E divide the line AC in the ratio of x:y
so, that BE=xc+yax+y=x⋅BDl+y⋅BFkx+y
⇒BE−xl(x+y)BD−yk(x+y)BF=0
Since, D,E and F are collinear.
Sum of coefficient must be zero.
hence, 1−xl(x+y)−yk(x+y)=0
⇒(x+y)−xl−yk=0impliex+y=xl+yk
⇒x(1−1l)=y(1k−1)⇒x(l−1l)=y(1−kk)
⇒ll−1⋅yx⋅k−1k=1
⇒BDDC⋅CEAE⋅AFBF=1 [using Eqs. (i), (ii) and (iii)].
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
If D,E,andF are three points on the sides BC,AC,andAB of a triangle ABC such that AD,BE,andCF are concurrent, then show that BD⋅CE⋅AF=DC⋅EA⋅FB .
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC show that the BDCD=CEAE=AFBF=−1
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIf D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of ΔABC , find the co-ordinates of point A , B and C .
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC and G is the centroid of the triangle, then −−→GD+−−→GE+−−→GF=
View Solution
