In a four-dimensional space where unit vectors along the axes are ˆi,ˆj,ˆkandˆl,anda1,a2,a3,a4 are four non-zero vectors such that no vector can be expressed as a linear combination of other (λ−1)(a1−a2)+μ(a2+a3)+γ(a3+a4−2a2)+a3+δa4=0, then
(a) λ=1
(b) μ=−23
(c) γ=23
(d) δ=13
The correct Answer is:A, B, D
To solve the given problem, we need to analyze the equation provided and find the values of the parameters λ,μ,γ, and δ under the condition that the vectors a1,a2,a3, and a4 are linearly independent.
1. Write the given equation:
(λ−1)(a1−a2)+μ(a2+a3)+γ(a3+a4−2a2)+a3+δa4=0
2. Expand the equation:
(λ−1)a1−(λ−1)a2+μa2+μa3+γa3+γa4−2γa2+a3+δa4=0
3. Combine like terms:
- Coefficient of a1: λ−1
- Coefficient of a2: −(λ−1)+μ−2γ
- Coefficient of a3: μ+γ+1
- Coefficient of a4: γ+δ
Thus, we have:
Coefficient of a1:λ−1=0Coefficient of a2:−(λ−1)+μ−2γ=0Coefficient of a3:μ+γ+1=0Coefficient of a4:γ+δ=0
4. Solve for λ:
From the first equation:
λ−1=0⟹λ=1
5. Substitute λ into the second equation:
−(1−1)+μ−2γ=0⟹μ−2γ=0⟹μ=2γ
6. Substitute μ into the third equation:
2γ+γ+1=0⟹3γ+1=0⟹γ=−13
7. Find μ:
Using μ=2γ:
μ=2(−13)=−23
8. Find δ:
From the fourth equation γ+δ=0:
−13+δ=0⟹δ=13
Summary of Results:
- λ=1
- μ=−23
- γ=−13
- δ=13
(λ−1)(a1−a2)+μ(a2+a3)+γ(a3+a4−2a2)+a3+δa4=0
(λ−1)a1−(λ−1)a2+μa2+μa3+γa3+γa4−2γa2+a3+δa4=0
- Coefficient of a1: λ−1
- Coefficient of a2: −(λ−1)+μ−2γ
- Coefficient of a3: μ+γ+1
- Coefficient of a4: γ+δ
Coefficient of a1:λ−1=0Coefficient of a2:−(λ−1)+μ−2γ=0Coefficient of a3:μ+γ+1=0Coefficient of a4:γ+δ=0
From the first equation:
λ−1=0⟹λ=1
−(1−1)+μ−2γ=0⟹μ−2γ=0⟹μ=2γ
2γ+γ+1=0⟹3γ+1=0⟹γ=−13
Using μ=2γ:
μ=2(−13)=−23
From the fourth equation γ+δ=0:
−13+δ=0⟹δ=13
- λ=1
- μ=−23
- γ=−13
- δ=13
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
If a1,a2,a3,a4,a5 are consecutive terms of an arithmetic progression with common difference 3, then the value of ∣∣ ∣ ∣∣a23a2a1a24a3a2a25a4a3∣∣ ∣ ∣∣ is
View SolutionIf a0,a1,a2,… are the coefficients in the expansion of
(1+x+x2)n in ascending powers of x, prove that
a0a2−a1a3+a2a4−…+a2n−2a2n=an+1 .
View SolutionIf log(1−x+x2)=a1x+a2x2+a3x3+…
then a3+a6+a9+.. is equal to
View SolutionMake the constraint relation between a1,a2 and a3
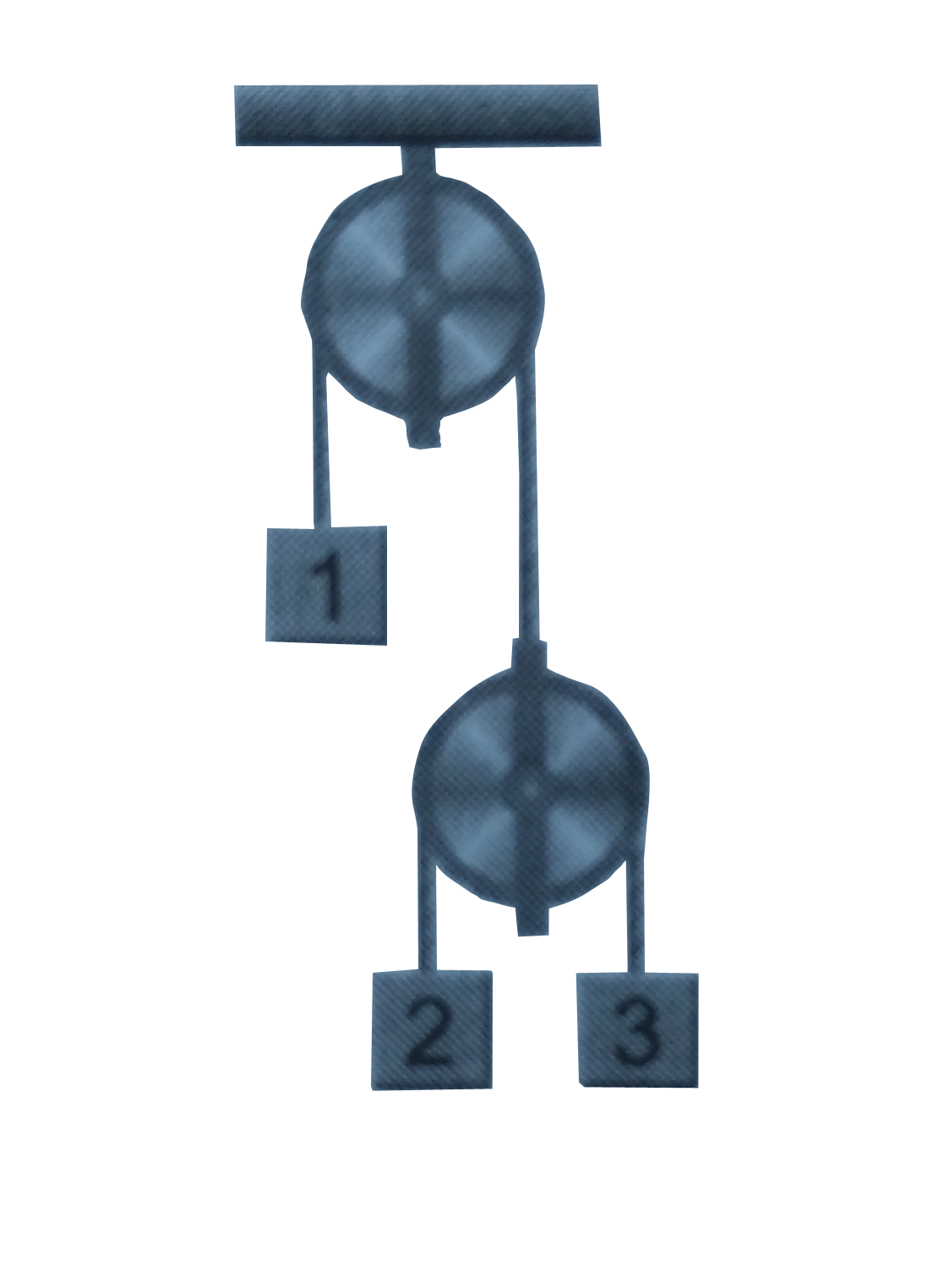
View SolutionIf a1,a2,a3,a4,a5 are in HP, then a1a2+a2a3+a3a4+a4a5 is equal to
View SolutionIt a1,a2,a3a4 be in G.P. then prove that (a2−a3)2+(a3−a1)2+(a4−a2)2=(a1−a4)2
View SolutionIf a1,a2,a3 are in arithmetic progression and d is the common diference, then tan−1(d1+a1a2)+tan−1(d1+a2a3)=
View SolutionIf a2a3a1a4=a2+a3a1+a4=3(a2−a3a1−a4), then a1,a2,a3,a4 are in
View SolutionIf a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionIf a1anda2 are two non- collinear unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View Solution

