If C is the middle point of AB and P is any point outside AB, then
PA+PB=PC
PA+PB=2PC
PA+PB+PC=0
PA+PB+2PC=0
The correct Answer is:B
To solve the problem, we need to prove that if C is the midpoint of AB and P is any point outside AB, then →PA+→PB=2→PC.
1. Define Points and Vectors:
Let the position vectors of points A, B, C, and P be represented as:
- →A=→0 (position vector of A)
- →B=→b (position vector of B)
- Since C is the midpoint of AB, we have:
→C=→A+→B2=→0+→b2=→b2
- Let the position vector of point P be →P.
2. Calculate Vectors PA and PB:
The vector from P to A is given by:
→PA=→A−→P=→0−→P=−→P
The vector from P to B is given by:
→PB=→B−→P=→b−→P
3. Add Vectors PA and PB:
Now, we add →PA and →PB:
→PA+→PB=−→P+(→b−→P)=→b−2→P
4. Calculate Vector PC:
The vector from P to C is given by:
→PC=→C−→P=→b2−→P
5. Calculate Twice Vector PC:
Now, we calculate 2→PC:
2→PC=2(→b2−→P)=→b−2→P
6. Equate the Two Results:
From steps 3 and 5, we have:
→PA+→PB=→b−2→P
2→PC=→b−2→P
Therefore, we conclude that:
→PA+→PB=2→PC
Conclusion:
We have proved that →PA+→PB=2→PC.
Let the position vectors of points A, B, C, and P be represented as:
- →A=→0 (position vector of A)
- →B=→b (position vector of B)
- Since C is the midpoint of AB, we have:
→C=→A+→B2=→0+→b2=→b2
- Let the position vector of point P be →P.
The vector from P to A is given by:
→PA=→A−→P=→0−→P=−→P
The vector from P to B is given by:
→PB=→B−→P=→b−→P
Now, we add →PA and →PB:
→PA+→PB=−→P+(→b−→P)=→b−2→P
The vector from P to C is given by:
→PC=→C−→P=→b2−→P
Now, we calculate 2→PC:
2→PC=2(→b2−→P)=→b−2→P
From steps 3 and 5, we have:
→PA+→PB=→b−2→P
2→PC=→b−2→P
→PA+→PB=2→PC
We have proved that →PA+→PB=2→PC.
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
If C is the mid point of AB and P is any point outside AB then (A) −−→PA+−−→PB+−−→PC=0 (B) −−→PA+−−→PB+2−−→PC=→0 (C) −−→PA+−−→PB=−−→PC (D) −−→PA+−−→PB=2−−→PC
View SolutionIf C is the mid point of AB and P is any point outside AB then (A) −−→PA+−−→PB+−−→PC=0 (B) −−→PA+−−→PB+2−−→PC=→0 (C) −−→PA+−−→PB=−−→PC (D) −−→PA+−−→PB=2−−→PC
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
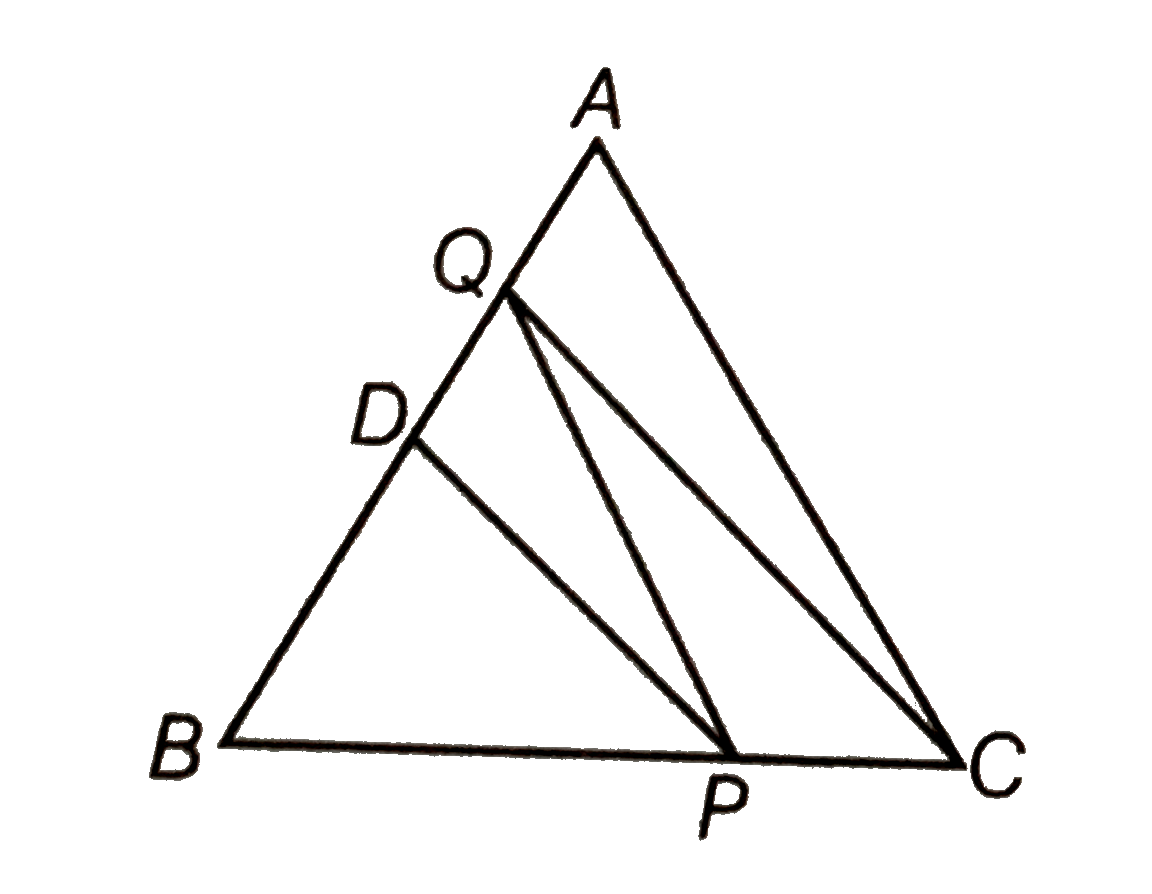
View SolutionIn triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View SolutionIn the adjoining figure
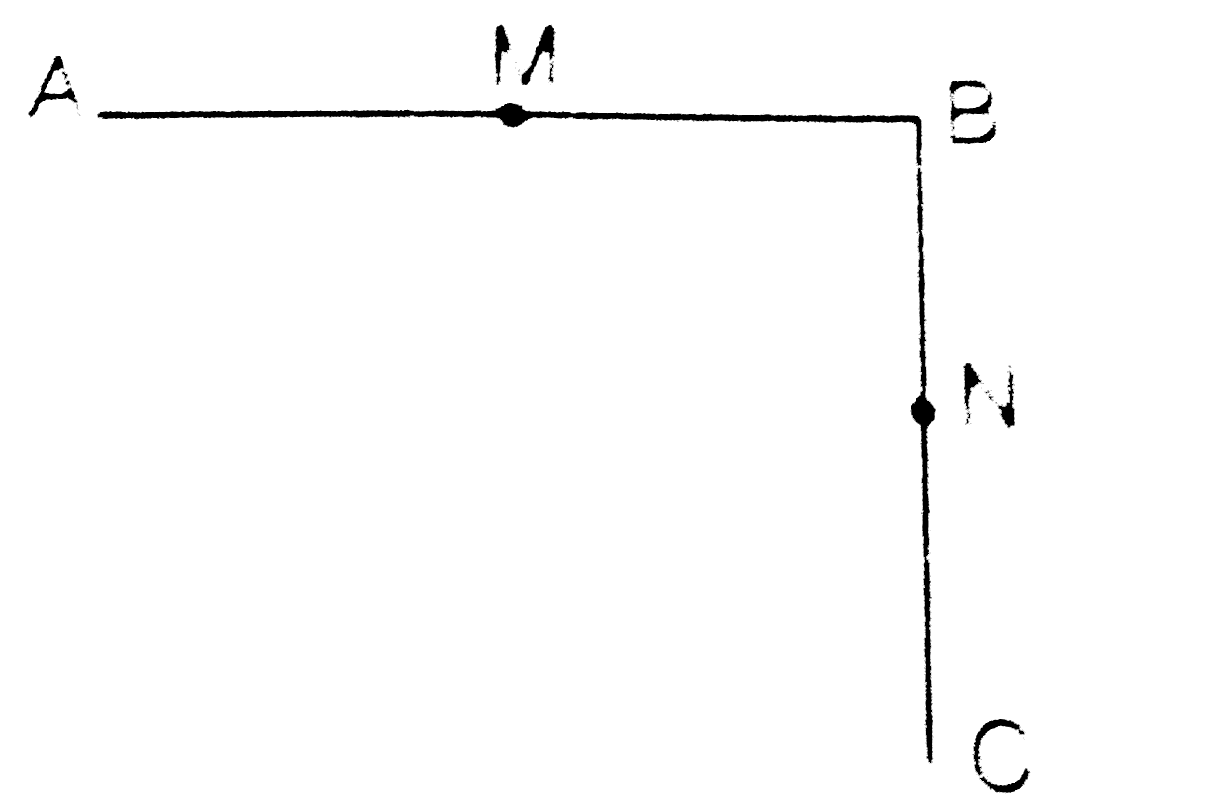
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionAB is vertical tower. The point A is on the ground and C is the middle point of AB. The part CB subtend an angle α at a point P on the ground. If AP=nAB, then tanα=
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View Solution
