If A={x:|x|<2},B={x:|x−5|≤2},
C={x:|x|>x}andD={x:|x|<x}
The number of integral values in A∩D is
A
2
B
4
C
6
D
0
Video Solution
Text Solution
The correct Answer is:D
A={x:|x|<2}={x:−2<x<2}=(−2,2)
B={x:|x−5|≤2}={x:−2≤x−5≤2}
={x:3≤x≤7}=[3,7]
C={x:|x|>x}={x:x<0}=(−∞,0)
and D={x:|x|<x}=ϕ
A∩D=(−2,2)∩ϕ=ϕ
∴ Number of integral values in A∩D is 0.
|
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 1
11 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 2
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
Similar Questions
Knowledge Check
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A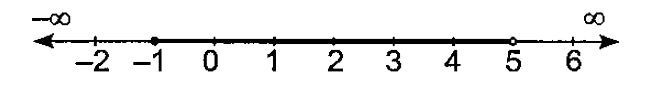 B
B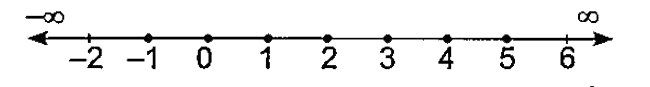 C
C D
D
The number of integral solutions of x2−3x−4<0, is
View SolutionThe number of intergal values of x if 5x−1<(x+1)2<7x−3 is
View SolutionThe number of integral value of x satistying √x2+10x−16<x−2 is
View SolutionC={x:x is a composite number and 5≤x≤21}
View SolutionGiven A={x:−1<x≤5,x∈R}andB={x:−4≤x<3,x∈R}.
Represent on different number line :
A - B
View SolutionGiven : A={x:3<2x−1<9,x∈R},B={x:11≤3x+2≤23,x∈R}
where R is the set of real numbers.
Represent A and B on number lines
View SolutionGiven A={x:−1<x≤5,x∈R}andB={x:−4≤x<3,x∈R}.
Represent on different number line :
A'∩B
View Solution
