Let and be the roots of the equation . If , the value of (where [.] denotes the greatest integer function) is ____
The correct Answer is:7
To solve the problem step by step, we will analyze the given polynomial equation and apply Vieta's formulas to find the required value of λ.
Step 1: Identify the roots and apply Vieta's formulas
The given polynomial is:
8x3+1001x+2008=0
Let the roots be r, s, and t. According to Vieta's formulas:
- The sum of the roots r+s+t=−coefficient of x2coefficient of x3=0
- The sum of the products of the roots taken two at a time rs+rt+st=coefficient of xcoefficient of x3=10018
- The product of the roots rst=−constant termcoefficient of x3=−20088=−251
Step 2: Define new variables for sums of pairs of roots
Let:
a=r+s,b=s+t,c=t+r
From the first step, we know:
a+b+c=(r+s)+(s+t)+(t+r)=2(r+s+t)=0
Step 3: Use the identity for the sum of cubes
We use the identity:
a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−ac−bc)
Since a+b+c=0, we have:
a3+b3+c3=3abc
Step 4: Calculate abc
We know:
abc=(r+s)(s+t)(t+r)
Expanding this:
abc=(r+s)(s+t)(t+r)=(r+s+t)(rs+rt+st)−rst
Since r+s+t=0, this simplifies to:
abc=−rst=251
Step 5: Calculate a3+b3+c3
Thus:
a3+b3+c3=3abc=3×251=753
Step 6: Relate to λ
We are given:
99λ=a3+b3+c3=753
Therefore:
λ=75399
Step 7: Simplify λ
Calculating 75399:
λ=7.60606060606…
Step 8: Apply the greatest integer function
The greatest integer function (λ) gives us:
(λ)=7
Final Answer
The value of (λ) is:
7
The given polynomial is:
8x3+1001x+2008=0
Let the roots be r, s, and t. According to Vieta's formulas:
- The sum of the roots r+s+t=−coefficient of x2coefficient of x3=0
- The sum of the products of the roots taken two at a time rs+rt+st=coefficient of xcoefficient of x3=10018
- The product of the roots rst=−constant termcoefficient of x3=−20088=−251
Let:
a=r+s,b=s+t,c=t+r
From the first step, we know:
a+b+c=(r+s)+(s+t)+(t+r)=2(r+s+t)=0
We use the identity:
a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−ac−bc)
Since a+b+c=0, we have:
a3+b3+c3=3abc
We know:
abc=(r+s)(s+t)(t+r)
Expanding this:
abc=(r+s)(s+t)(t+r)=(r+s+t)(rs+rt+st)−rst
Since r+s+t=0, this simplifies to:
abc=−rst=251
Thus:
a3+b3+c3=3abc=3×251=753
We are given:
99λ=a3+b3+c3=753
Therefore:
λ=75399
Calculating 75399:
λ=7.60606060606…
The greatest integer function (λ) gives us:
(λ)=7
The value of (λ) is:
7
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matching Type Questions)2videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATCH TYPE2videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Passage Based Questions)21videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)17videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam2videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
Column I contains rational algebraic expressions and Column II contains possible integers which lie in their ragne. Match the entries of Column I with one or more entries of the elements of Column II.
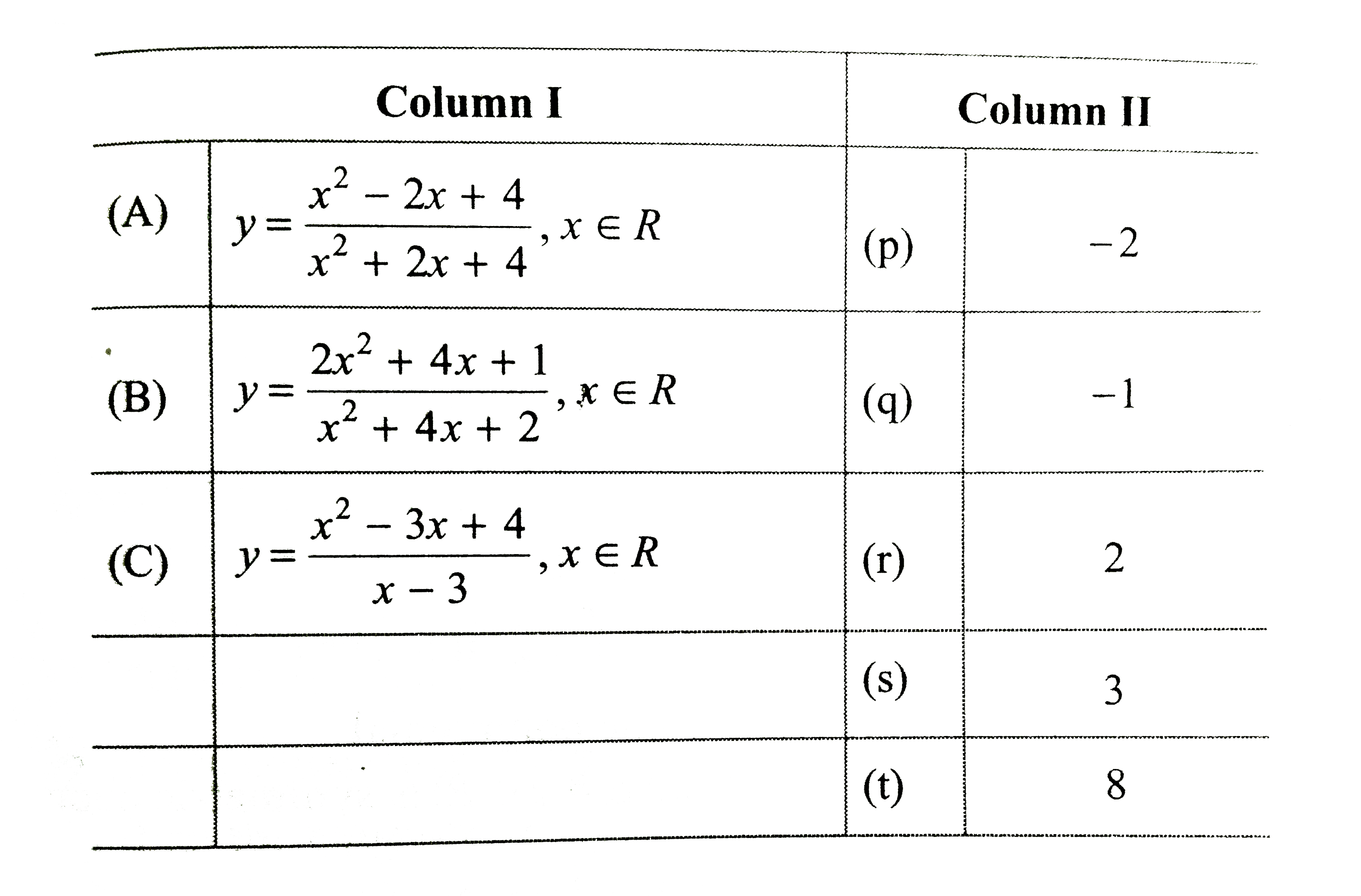 03:58View Solution
03:58View SolutionMatch the following Column I to Column II
 03:58View Solution
03:58View SolutionIf G and L are the greatest and least values of the expression2x2−3x+22x2+3x+2,xεR respectively.
The least value of G100+L100 is
(a) 2100 (b) 3100 (c) 7100 (d) none of these03:38View SolutionThe line parallel to the x-axis and passing through the intersection of the lines ax+2by+3b=0 and bx−2y−3a=0 , where (a,b)≠(0,0) , is above the x-axis at a distance of 3/2 units from it above the x-axis at a distance of 2/3 units from it below the x-axis at a distance of 3/2 units from it below the x-axis at a distance of 2/3 units from it
01:58View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
03:32View SolutionLet r,s,andt be the roots of equation 8x3+1001x+2008=0. Then find the value of (r+s)3+(s+t)3+(t+r)3 .
03:11View SolutionLet r,s and t be the roots of the equation, 8x3+1001x+2008=0. The value of (r+s)3+(s+t)3+(t+r)3is
03:11View SolutionLet r,s and t be the roots of the equation 8x3+1001x+2008=0 and if 99λ=(r+s)3+(s+t)3+(t+r)3, the value of [λ] is (where [.] denotes the greatest integer function)
03:18View SolutionIf s=t+√r3q, what is the value of r in terms of q, s and t ?
05:13View SolutionLet r,s,andt be the roots of equation 8x3+1001x+2008=0. Then find the value of (r+s)3+(s+t)3+(t+r)3 .
05:32View Solutionमाना r,s और t समाकरण 8x3+1001x+2008=0 के मूल है, तो (r+s)3+(s+t)3+(r+t)3+=
04:12View Solutionमाना r,s और t समाकरण 8x3+1001x+2008=0 के मूल है, तो (r+s)3+(s+t)3+(r+t)3+=
03:31View SolutionLet r,s,andt be the roots of equation 8x3+1001x+2008=0. Then find the value of .
06:12View SolutionLet r,s,andt be the roots of equation 8x3+1001x+2008=0. Then find the value of (r+s)3+(s+t)3+(t+r)3 .
03:55View SolutionLet r,sandt be the roots of equation 8x3+1001x+2008=0. Then find the value of (r+s)3+(s+t)3+(t+r)3 is .
View SolutionLet r,s and t be the roots of the equation 8x3+1001x+2008=0 and if 99λ=(r+s)3+(s+t)3+(t+r)3, the value of [λ] is (where [.] denotes the greatest integer function)
01:55View Solution
