Two conducting slabs of heat conductivity K1 and K2 are joined as shown in fig. The temp. at ends of the slabs are θ1 and θ2(θ1>θ2) the, final temp. (θm) of junction is :

K1θ1+K2θ2K1+K2
K1θ2+K2θ1K1+K2
K1θ2−K2θ1K1+K2
None
The correct Answer is:A
Q=K1A(θ1−θ)td=K2A(θ−θ2)td
Or K1θ1−K1θ=K2θ−K2θ2
K1θ1+K2θ2=K1θ+K2θ
θ=K1θ1+K2θ2K1+K2
Similar Questions
Prove that 1+tan2θtanθ=sec2θ.
View SolutionIf tan2θtanθ=1,thenθ=
View SolutionSolve sin2θtanθ+cos2θcotθ−sin2θ=1+tanθ+cotθ
View SolutionSolve tanθ+tan2θ+tanθ⋅tan2θ⋅tan3θ=1
View SolutionTwo materials having coefficients of thermal conductivity '3k' and 'k' and thickness 'd' and '3d' respectively, are joined to form a slab as shown in the figures. The temperatures of the outer surfaces are θ2 and θ1 respectively (θ2>θ2). The temperature at the interface is :
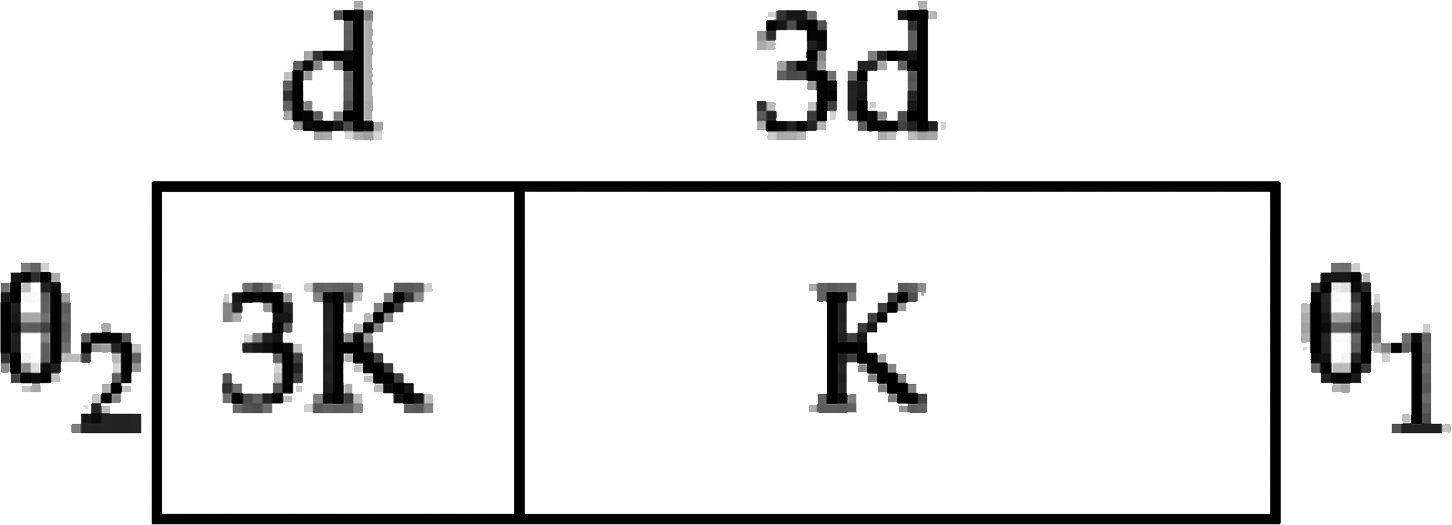
View SolutionProve that sin(2θ)1−cos2θ=cotθ
View SolutionProve that cosθ(tanθ+2)(2tanθ+1)=2secθ+5sinθ
View Solutionsinθ+sin2θ1+cosθ+cos2θ=tanθ.
View SolutionProve that 1−cos2θsin2θ=tanθ.
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View Solution
