Initially plane of coil is parallel to the uniform magnetic field B. In time Δt it makes to perpendicular to the magnetic field, then charge flows in Δt depends on this time as -
∝Δt
∝1Δt
∝(Δt)0
∝(Δt)2
The correct Answer is:C
To solve the problem, we need to analyze the situation where a coil is rotating in a magnetic field and determine how the charge that flows through the coil depends on the time taken for this rotation.
1. Understanding the Initial Setup:
- The coil is initially parallel to the magnetic field B. In this position, the magnetic flux through the coil is zero because the angle between the magnetic field and the normal to the coil is 0∘.
2. Change in Orientation:
- The coil rotates from being parallel to the magnetic field to being perpendicular to it. When the coil is perpendicular to the magnetic field, the magnetic flux through the coil is at its maximum. The angle between the magnetic field and the normal to the coil is 90∘.
3. Magnetic Flux Calculation:
- The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the coil and θ is the angle between the magnetic field and the normal to the coil.
- Initially, Φinitial=0 (when parallel) and finally, Φfinal=B⋅A (when perpendicular).
4. Change in Magnetic Flux:
- The change in magnetic flux ΔΦ as the coil rotates from parallel to perpendicular is:
ΔΦ=Φfinal−Φinitial=B⋅A−0=B⋅A
5. Induced EMF:
- According to Faraday's law of electromagnetic induction, the induced EMF E in the coil is given by the rate of change of magnetic flux:
E=−dΦdt
- The average induced EMF during the time Δt is:
E=ΔΦΔt=B⋅AΔt
6. Current Calculation:
- The current I flowing through the coil can be expressed as:
I=ER=B⋅AR⋅Δt
- Here, R is the resistance of the coil.
7. Charge Flow Calculation:
- The total charge Q that flows through the coil during the time Δt is given by:
Q=I⋅Δt=(B⋅AR⋅Δt)⋅Δt=B⋅AR
8. Conclusion:
- From the above calculations, we see that the charge Q is independent of the time Δt taken for the rotation. Thus, we conclude that the charge depends only on the orientation of the coil and not on the time taken for the rotation.
Final Answer:
The charge Q that flows in time Δt is independent of Δt and can be expressed as:
Q∝Δt0
- The coil is initially parallel to the magnetic field B. In this position, the magnetic flux through the coil is zero because the angle between the magnetic field and the normal to the coil is 0∘.
- The coil rotates from being parallel to the magnetic field to being perpendicular to it. When the coil is perpendicular to the magnetic field, the magnetic flux through the coil is at its maximum. The angle between the magnetic field and the normal to the coil is 90∘.
- The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the coil and θ is the angle between the magnetic field and the normal to the coil.
- Initially, Φinitial=0 (when parallel) and finally, Φfinal=B⋅A (when perpendicular).
- The change in magnetic flux ΔΦ as the coil rotates from parallel to perpendicular is:
ΔΦ=Φfinal−Φinitial=B⋅A−0=B⋅A
- According to Faraday's law of electromagnetic induction, the induced EMF E in the coil is given by the rate of change of magnetic flux:
E=−dΦdt
- The average induced EMF during the time Δt is:
E=ΔΦΔt=B⋅AΔt
- The current I flowing through the coil can be expressed as:
I=ER=B⋅AR⋅Δt
- Here, R is the resistance of the coil.
- The total charge Q that flows through the coil during the time Δt is given by:
Q=I⋅Δt=(B⋅AR⋅Δt)⋅Δt=B⋅AR
- From the above calculations, we see that the charge Q is independent of the time Δt taken for the rotation. Thus, we conclude that the charge depends only on the orientation of the coil and not on the time taken for the rotation.
The charge Q that flows in time Δt is independent of Δt and can be expressed as:
Q∝Δt0
Similar Questions
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
In the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionThe path of a charged particle in a uniform magnetic field, when the velocity and the magnetic field are perpendicular to each other is a
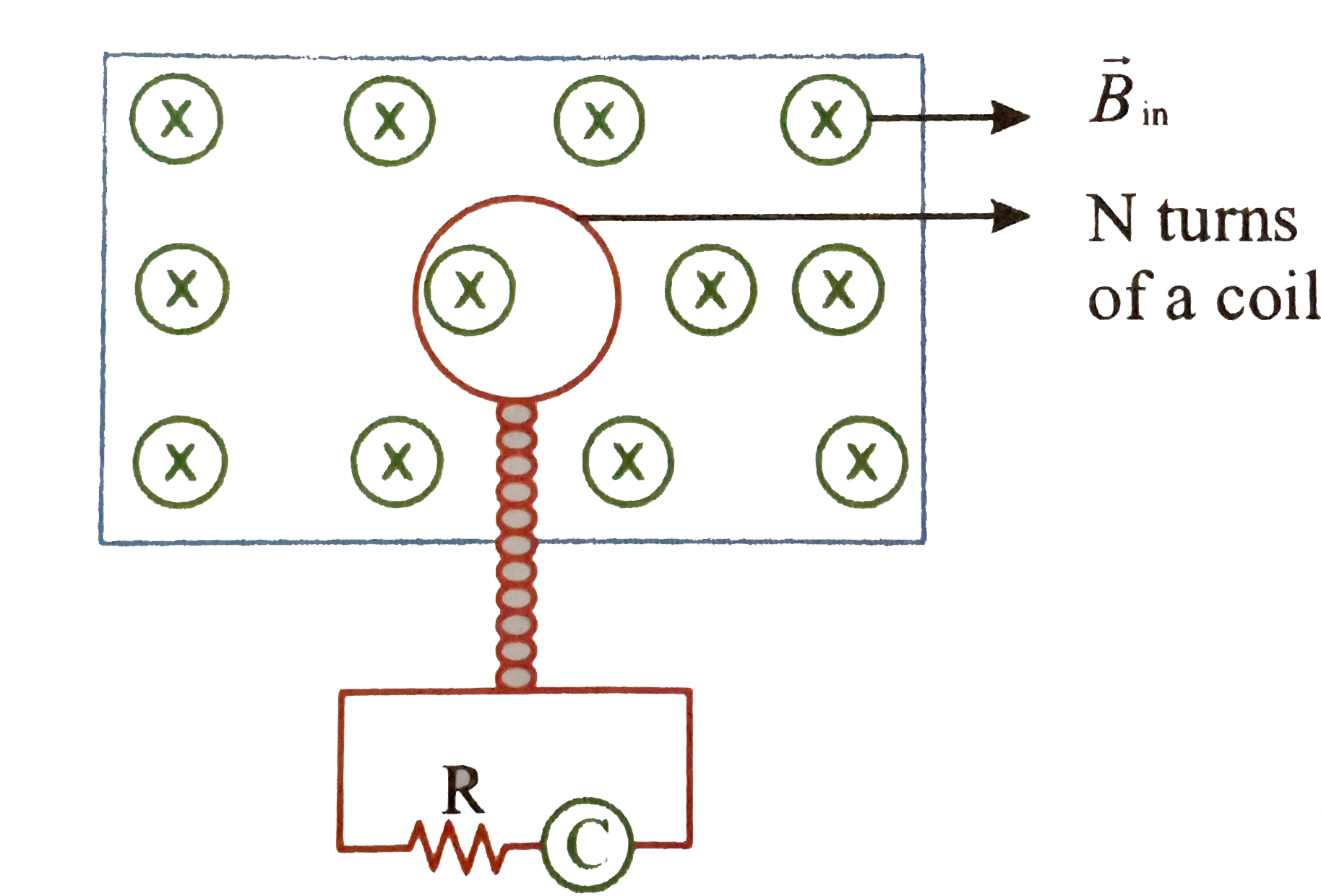
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
View SolutionAssertion A charged particle is rotating in a circular path in uniform magnetic field. Then, plane of circle is perpendicular to the magnetic field.
Reason Circular motion is a two-dimensional motion.
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
View SolutionA rectangular coil of area A rotates in a uniform magnetic field B with angular velocity about an axis perpendicular to the field, initially the plane of coil is perpendicular to the field,then the avarage induced e.m.f. after rotating by 90° is
View Solution
