Iron exhibits b structure at roomj temperature. Above 900∘C, it transformers to f structure. The ratio of density of iron at room temperature to that at 900∘C (assuming molar mass and atomic radius of iron remains constant with temperature) is
3√34√2
4√33√2
√3√2
12
The correct Answer is:A
To find the ratio of the density of iron at room temperature (where it exhibits a BCC structure) to that at 900°C (where it transforms to an FCC structure), we can follow these steps:
Step 1: Understand the structures and their parameters
- BCC (Body-Centered Cubic):
- Number of atoms per unit cell (Z) = 2
- Edge length (A) = 4R√3
- FCC (Face-Centered Cubic):
- Number of atoms per unit cell (Z) = 4
- Edge length (A) = 2√2R
Step 2: Write the formula for density
The density (ρ) of a crystal structure can be calculated using the formula:
ρ=Z⋅MNa⋅A3
Where:
- Z = number of atoms per unit cell
- M = molar mass
- Na = Avogadro's number
- A = edge length of the unit cell
Step 3: Calculate the density for BCC and FCC
- Density at room temperature (BCC):
ρBCC=ZBCC⋅MNa⋅A3BCC=2⋅MNa⋅(4R√3)3
- Density at 900°C (FCC):
ρFCC=ZFCC⋅MNa⋅A3FCC=4⋅MNa⋅(2√2R)3
Step 4: Set up the ratio of densities
We need to find the ratio ρBCCρFCC:
ρBCCρFCC=2⋅MNa⋅(4R√3)34⋅MNa⋅(2√2R)3
Step 5: Simplify the ratio
Since the molar mass M and Avogadro's number Na cancel out, we have:
ρBCCρFCC=24⋅(2√2R)3(4R√3)3
=12⋅(2√2)3⋅R3(64R33√3)
=12⋅16√2R3⋅3√364R3
=12⋅48√664
=48√6128=3√68
Step 6: Final Ratio
Thus, the final ratio of the density of iron at room temperature to that at 900°C is:
3√68
- BCC (Body-Centered Cubic):
- Number of atoms per unit cell (Z) = 2
- Edge length (A) = 4R√3
- FCC (Face-Centered Cubic):
- Number of atoms per unit cell (Z) = 4
- Edge length (A) = 2√2R
The density (ρ) of a crystal structure can be calculated using the formula:
ρ=Z⋅MNa⋅A3
Where:
- Z = number of atoms per unit cell
- M = molar mass
- Na = Avogadro's number
- A = edge length of the unit cell
- Density at room temperature (BCC):
ρBCC=ZBCC⋅MNa⋅A3BCC=2⋅MNa⋅(4R√3)3
ρFCC=ZFCC⋅MNa⋅A3FCC=4⋅MNa⋅(2√2R)3
We need to find the ratio ρBCCρFCC:
ρBCCρFCC=2⋅MNa⋅(4R√3)34⋅MNa⋅(2√2R)3
Since the molar mass M and Avogadro's number Na cancel out, we have:
ρBCCρFCC=24⋅(2√2R)3(4R√3)3
=12⋅(2√2)3⋅R3(64R33√3)
=12⋅16√2R3⋅3√364R3
=12⋅48√664
=48√6128=3√68
Thus, the final ratio of the density of iron at room temperature to that at 900°C is:
3√68
Similar Questions
The temperature at which the root mean squres speed of a gas will be half its value at 0∘C is (assume the pressure remains constant)
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
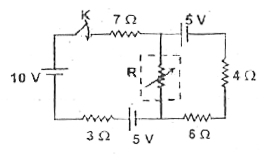 View Solution
View SolutionWhen heated above 916∘C, iron changes its bcc crystalline from to fcc without the change in the radius of atom . The ratio of density of the crystal before heating and after heating is :
View SolutionThe maximum temperature 1550∘C is obtained in the _____ region of the blast furnace used in the the extraction of iron.
View SolutionAt what temperature will a given mass of a gas occupy a volume of 200L, if it occupies a volume of 260L at a temperature of 30∘C, pressure remaining constant?
View SolutionAir is filled at 60∘C in a vessel of open mouth. The vessle is heated to a temperature T so that 1/4th of air escapes. Assuming the volume of vessel remaining constant, the value of T is
View SolutionAir is filled at 60∘C in a vessel of open mouth. The vessel is heated to a temperature T so that 1/4th of air escapes. Assuming the volume of vessel remaining constant, the value of T is
View SolutionThe γ-form of iron has f structure (edge length 386±) and β-form has b structure (edge length 290±). The ratio of density in γ-form and β-form is
View SolutionWhat is the percentage change in length of 1m iron rod it its temperature changes by 100∘C.α for iron is 2×10−5/∘C.
View SolutionAt what temperature will the speed of sound in hydrogen be the same as in oxygen at 100∘C ? Molar Masses of oxygen and hydrogen are in the ratio 16:1 .
View Solution
