A thermocouple of negligible resistance produces an emf fo 40μV/∘C in the linear range of temperature. A galvanometer of resistance 10Ω whose sensitivity is 1μA/÷ is employed with the thermocouple. The smallest value of temperature difference that can be detected by the system will
0.25∘C
0.5∘C
1∘C
0.1∘C
The correct Answer is:A
To solve the problem, we need to determine the smallest temperature difference that can be detected by the system consisting of a thermocouple and a galvanometer.
1. Understand the Given Data:
- The thermocouple produces an emf of 40μV/∘C.
- The galvanometer has a resistance of 10Ω and a sensitivity of 1μA/div.
2. Calculate the Current for 1 Degree Celsius:
- The emf produced by the thermocouple for a temperature difference of 1∘C is 40μV.
- Using Ohm's Law, the current (I) through the galvanometer can be calculated as:
I=VR=40μV10Ω
- Converting 40μV to volts gives:
I=40×10−6V10Ω=4×10−6A=4μA
3. Determine the Current Sensitivity:
- The galvanometer's sensitivity is 1μA/div. This means that for every 1μA of current, the galvanometer will show a deflection of 1 division.
4. Calculate the Temperature Difference for 1 Microampere:
- Since 4μA corresponds to a temperature difference of 1∘C, we can find the temperature difference corresponding to 1μA:
Temperature difference=1∘C4μA=0.25∘C
5. Conclusion:
- The smallest temperature difference that can be detected by the system is 0.25∘C.
Final Answer:
The smallest value of temperature difference that can be detected by the system is 0.25∘C.
- The thermocouple produces an emf of 40μV/∘C.
- The galvanometer has a resistance of 10Ω and a sensitivity of 1μA/div.
- The emf produced by the thermocouple for a temperature difference of 1∘C is 40μV.
- Using Ohm's Law, the current (I) through the galvanometer can be calculated as:
I=VR=40μV10Ω
- Converting 40μV to volts gives:
I=40×10−6V10Ω=4×10−6A=4μA
- The galvanometer's sensitivity is 1μA/div. This means that for every 1μA of current, the galvanometer will show a deflection of 1 division.
- Since 4μA corresponds to a temperature difference of 1∘C, we can find the temperature difference corresponding to 1μA:
Temperature difference=1∘C4μA=0.25∘C
- The smallest temperature difference that can be detected by the system is 0.25∘C.
The smallest value of temperature difference that can be detected by the system is 0.25∘C.
Similar Questions
A galvanometer of resistance 40Ω can measure a current of 10mA To convert it into a voltmeter of range 8V the required resistance is ___________ Ω.
View SolutionA galvanometer has a xoil of resistance 100(Ω)showing a full-scale deflection at 50(mu)A. What resistance should be added to use it as (a) a voltmeter of range 50 V (b) an ammeter of range 10 mA?
View SolutionA galvanometer of 50Ω resistance when connected across the terminals of a battery of emf 2V along with the resistance 200Ω the deflection produced in the galvanometer is 10 divisions. If the total number of divisions on the galvanometer ·scale on either side of central zero is 30, then the maximum current that can pass through the galvanometer is
View SolutionA galvanometer of resistance 10Ω shows full scale deflection for current 100 mA. The resistance that needs to be connected in series with the galvanometer so that it can be used to measure potential difference in the range 0-100 V is (in Ohm):
View SolutionAn accumulator of emf 2V and negligible internal resistance is connected across a uniform wire of length 10 m and resistance 30Ω The appropriate terminals of a cell of emf 1.5V and internal resistance 1Ω is connected to one end of the wire and the other terminal of the cell is connected through a sensitive galvanometer to a slider on the wire. What is the length of the wire that will be required to produce zero deflection of the galvanometer? How will the balancing length change?
(a) When a coil of resistance 5Ω is placed in series with the accumulator.
(b) The cell of 1.5V is shunted with 5Ω resistor?
View SolutionThe temperature coefficient of resistance of tungsten is 4.5×10−3∘C−1 and that of germanium is −5×10−2∘C−1 . A tungsten wire of resistance 100Ω is connected in series with a germanium wire of resistance R. The value of R for which the resistance of combination does not change with temperature is .
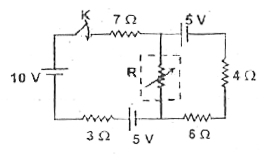
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
View SolutionE.M.F. of a thermocouple is 25 uV/.∘C A galvanometer whose resistance is 40omega, reads, 10−1A curren then minimum temperature which is determined by if will be
View SolutionNear room t emperature, the thermo emf of a copper constantan couple is 40μV per degree. What is the smallest temperature difference that can be detected with a single such couple and a galvanometer of 100 ohm resistance capable of detecting current as low 10−6 ampere?
View SolutionA capacitor of capacitance 10μF is connected to a resistance 2Ω and a battery of emf 5V of negligible interanl resistance. After 20μs of comleting the circuit find.
a. power delivered by the battery
b. power dissipated as heat
c. rate of energy stored in the capacitor
View Solution
