A galvanometer of resistance is shunted by a resistance . To keep the main current in the circuit uncharged, the resistnace to be put in series with the galvonmeter
The correct Answer is:D
To solve the problem, we need to find the resistance R that should be put in series with the galvanometer to keep the main current in the circuit unchanged when a shunt resistance S is connected in parallel with the galvanometer of resistance G.
1. Understand the Circuit Configuration:
- We have a galvanometer with resistance G.
- A shunt resistance S is connected in parallel with the galvanometer.
- A resistance R is connected in series with the combination of the galvanometer and the shunt.
2. Calculate the Equivalent Resistance of the Parallel Combination:
- The equivalent resistance Req of the galvanometer and the shunt can be calculated using the formula for resistors in parallel:
Req=G⋅SG+S
3. Total Resistance in the Circuit:
- The total resistance Rtotal in the circuit, which includes the series resistance R, is given by:
Rtotal=R+Req=R+G⋅SG+S
4. Setting Up the Equation:
- To keep the main current in the circuit unchanged, the total resistance after adding R must equal the resistance G of the galvanometer alone:
R+G⋅SG+S=G
5. Rearranging the Equation:
- Rearranging gives us:
R=G−G⋅SG+S
6. Finding a Common Denominator:
- To simplify, we can express R with a common denominator:
R=G(G+S)−G⋅SG+S
- This simplifies to:
R=G2G+S
7. Final Result:
- Thus, the resistance R that should be put in series with the galvanometer is:
R=G2G+S
- We have a galvanometer with resistance G.
- A shunt resistance S is connected in parallel with the galvanometer.
- A resistance R is connected in series with the combination of the galvanometer and the shunt.
- The equivalent resistance Req of the galvanometer and the shunt can be calculated using the formula for resistors in parallel:
Req=G⋅SG+S
- The total resistance Rtotal in the circuit, which includes the series resistance R, is given by:
Rtotal=R+Req=R+G⋅SG+S
- To keep the main current in the circuit unchanged, the total resistance after adding R must equal the resistance G of the galvanometer alone:
R+G⋅SG+S=G
- Rearranging gives us:
R=G−G⋅SG+S
- To simplify, we can express R with a common denominator:
R=G(G+S)−G⋅SG+S
- This simplifies to:
R=G2G+S
- Thus, the resistance R that should be put in series with the galvanometer is:
R=G2G+S
Similar Questions
A galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionA galvanometer of resistance 150 ohm is shunted such that only 1/11 of the main current flows through the galvanometer. The resistance of the shunt is, (in ohm)
View Solution
Knowledge Check
A galvanometer of resistance 70Ω, is converted to an ammeter by a shunt resistance r3=0.03Ω. The value of its resistance will become
A0.025ΩB0.022ΩC0.035ΩD0.030Ω
A galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View SolutionA galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View SolutionIn the circuit, shown the galvanometer G of resistance 60Ω is shifted by a resistance r=0.02Ω. The current through R is nearly 1A. The value of resistance R (in ohm) is nearly.
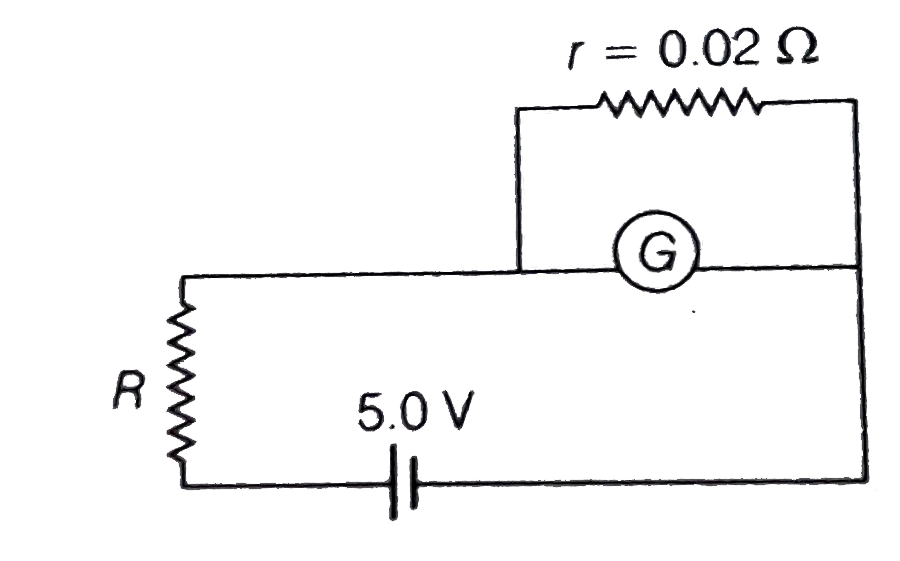
View SolutionWhen a current of 5mA is passed through a galvanometer having a coil of resistance 15Ω, it shows full sacle deflection. The value of the resistance to be put in series with the galvanometer to convert it into a voltmeter of range 0−10V is:
View SolutionA resistance box, a battery and a galvanometer of resistance G ohm are connected in series. the galvanometer is shunted by resistance of S ohm, find the change in resistance in the be required to maintain the current from the battery unchanged.
View SolutionA galvanometer of resistance 10Ω shows full scale deflection for current 100 mA. The resistance that needs to be connected in series with the galvanometer so that it can be used to measure potential difference in the range 0-100 V is (in Ohm):
View SolutionA voltmeter with a resistance 50×103Ω is used to measure voltage in a circuit. To increase its range to 3 times, the additional resistance to be put in series is
View Solution

