For the reaction N2+3H2→2NH3, if d[NH3]dt.=4×10−4 mol L−1s−1, the value of −d[H2]dt would be
1×10−4 mol L−1s−1
3×10−4molL−1s−1
4×10−4molL−1s−1
6×10−4molL−1s−1
The correct Answer is:B
To solve the problem, we need to relate the rates of change of the concentrations of the reactants and products in the given reaction:
N2+3H2→2NH3
We are given that the rate of formation of ammonia (NH3) is:
d(NH3)dt=4×10−4mol L−1s−1
We need to find the rate of decrease of hydrogen (H2), which is represented as:
−d(H2)dt
Step 1: Write the rate expressions based on stoichiometry
From the balanced chemical equation, we can express the rates of change of the concentrations as follows:
12d(NH3)dt=−13d(H2)dt
Step 2: Substitute the known value
We know that:
d(NH3)dt=4×10−4mol L−1s−1
Substituting this into the rate expression gives:
12(4×10−4)=−13d(H2)dt
Step 3: Calculate the left-hand side
Calculating the left-hand side:
12(4×10−4)=2×10−4mol L−1s−1
Step 4: Rearranging to find −d(H2)dt
Now we can rearrange the equation to find −d(H2)dt:
2×10−4=−13d(H2)dt
Multiplying both sides by -3 gives:
−3×2×10−4=d(H2)dt
d(H2)dt=−6×10−4mol L−1s−1
Step 5: Final answer
Thus, the value of −d(H2)dt is:
−d(H2)dt=6×10−4mol L−1s−1
Summary
The final answer is:
6×10−4mol L−1s−1
Similar Questions
For the reaction , N2+3H2→2NH3 if d[NH3]dt=2×10−4mol L−1s−1 , the value of −d[H2]dt would be
View SolutionFor the reaction N2+3H2→2NH3 if
Δ[NH3]Δt=2×10−4molL−1s−1, the value of −Δ[H2]Δt would be
View SolutionFor the reaction N2(g)+3H2(g)→2NH3(g) if Δ[NH3]Δt=4×10−4mol.l−1s−1, the value of −Δ[H2]Δt would be
View SolutionN2+3H2→NH3
View SolutionN2+3H2→NH3
View SolutionA+2B→C+D. If −d[A]dt=5×10−4 mol L−1s−1, then −d[B]dt is :
View SolutionKp for the reaction N2+3H2⇔2NH3 at 400∘C is 1.64×10−4atm−2. Find Kc.
View SolutionIn the hober's process of ammonia manufacture,
N2(g)+3H2(g)→2NH3(g)
the rate of appearance of NH3 is :
d[NH3]dt=2×10−4molL−1sec−1
The rates of the reaction expressed in terms of N2andH2 will be :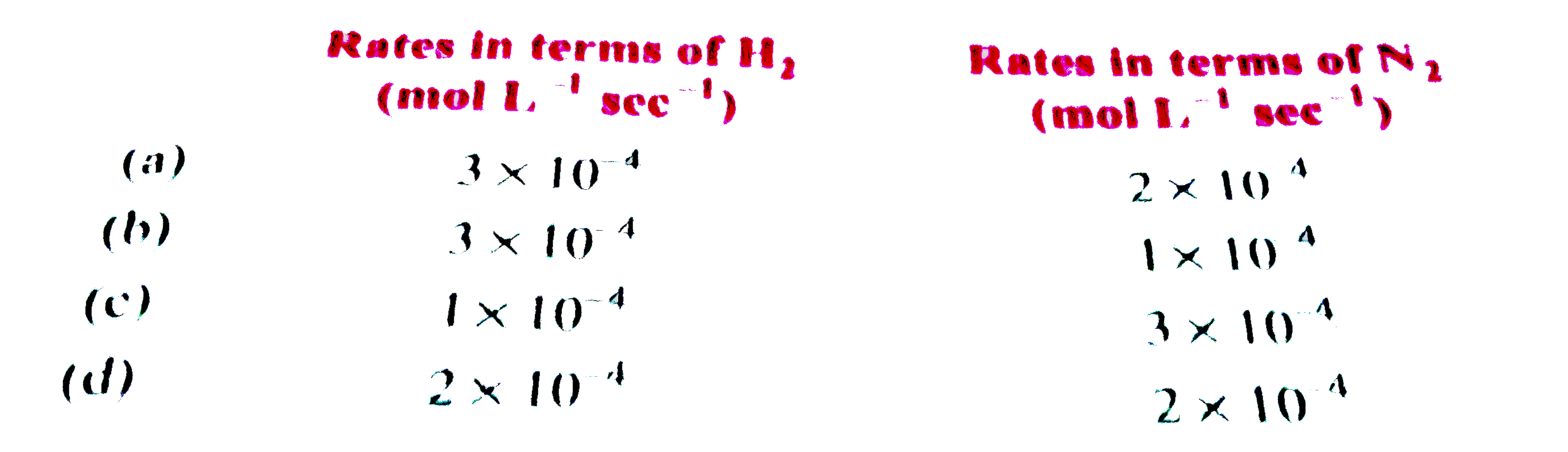
View SolutionFor the reaction
H2(g)+I2(g)→2HI(g), the rate of disappearance of H2 is 1.0×10−4molL−1s−1. The rate of appearance of HI will be
View SolutionIn a reaction N2(g)+3H2(g)→2NH3(g) rate of appearance of NH3 is 2.5×10−4molL−1sec−1 then rate of reaction and rate
of disappearance of H2 respectively is :-
View Solution
