Sand is being dropped on a conveyor belt at the rate of Mkg/s . The force necessary to kept the belt moving with a constant with a constant velocity of vm/s will be.
Mv2 newton
zero
Mv newton
2 Mv newton
The correct Answer is:C
Fext.=dpdt=d(mv)dt,
m = mass of system as conveyor belt with sand drops at time t.
Fext.=mdvdt+vdmdt
but v →constant so, dvdt=0
Fext=vdmdt=Mv
Fext is in direction of →v of belt.
OR
Since m.dvdt=Fext+Freaction ......(i)
Consider belt as a system with variable mass
dvdt=0,m=mass of systme at time t
Freaction=vrec.dmdt=−vdmdt ......(ii)
⇒ Fext.=v.dmdt=Mv.
→Fext is in direction of →v to keep belt moving with constant velocity.
Similar Questions
Gravel is dropped on a conveyor belt at the rate of 2 kg/s. The extra force required to keep the belt moving at 3ms−1 is
View SolutionA cart is moving with a velocity 20m/s. Sand is being dropped into the cart at the rate of 50 kg/min. The force required to move the cart with constant velocity will be :-
View SolutionGravels are dropped on a conveyor belt at the rate of 0.5 kg / sec . The extra force required in newtons to keep the belt moving at 2 m/sec is
View SolutionIn the block moves up with constant velocity v m/s. Find F
 View Solution
View SolutionSand drops from a stationary hopper at the rate of 5kg/s on to a conveyor belt moving with a constant speed of 2m/s. What is the force required to keep the belt moving and what is the power delivered by the motor, moving the belt?
View SolutionA suitcase is gently dropped on a conveyor belt moving at 3m/s. If the coefficient of friction between the belt and the suitcase is 0.5. Find the displacement of suitcase relative to conveyor belt before the slipping between the two is stopped (g=10m/s2)
View SolutionA suitcase is gently dropped on a conveyor belt moving at 3m/s. If the coefficient of friction between the belt and the suitcase is 0.5. Find the displacement of suitcase relative to conveyor belt before the slipping between the two is stopped (g=10m/s2)
View SolutionA point object is kept at the first focus of convex lens ,if the lens starts moving towards right will a constant velocity,th image will
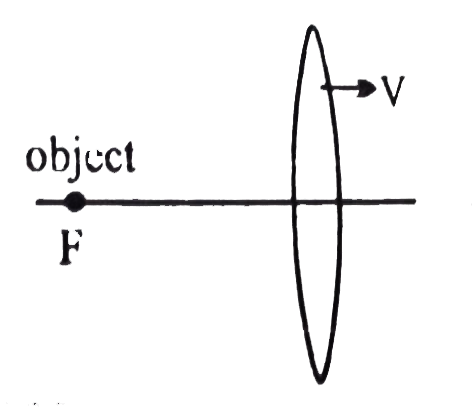 View Solution
View SolutionA package rest on a conveyor belt which is initially at rest . The belt is started and moves to the right for 1.3s with a constant acceleration of 2m/s2. The belt then moves with a constant deceleration a2 and comes to a stop after a total displacement of 2.2m . Knowing that the coefficient of friction between the package and the belt are μs=0.35 and μk=0.25 , determine (a) the deceleration a2 of the belt , (b) the displacement of the package relative to the belt as the belt comes to a stop. (g=9.8m/s2)
 View Solution
View SolutionWhat net force is required to maintain a 5,000 kg object moving at a constant velocity of magnitude 7,500 m / s ?
View Solution


