A 6 V battery is connected to the terminals of a 3 m long wire of uniform thickness and resistance of 100Ω. The difference of potential between two points on the wire separated by a distance of 50 cm will be
a 3 v
b 1v
c 1.5 v
d 2 v
The correct Answer is:B
To solve the problem step by step, we can follow these instructions:
Step 1: Identify the given values
- Voltage of the battery (V) = 6 V
- Length of the wire (L) = 3 m
- Resistance of the wire (R) = 100 Ω
- Distance between the two points on the wire (L') = 50 cm = 0.5 m
Step 2: Calculate the total current flowing through the circuit
Using Ohm's law, the current (I) can be calculated using the formula:
I=VR
Substituting the values:
I=6V100Ω=0.06A
Step 3: Determine the resistance of the segment of the wire (R')
To find the resistance of the 50 cm segment of the wire, we can use the formula for resistance:
R′=R⋅L′L
Where:
- R is the total resistance of the wire,
- L′ is the length of the segment we are interested in (0.5 m),
- L is the total length of the wire (3 m).
Substituting the values:
R′=100Ω⋅0.5m3m=503Ω≈16.67Ω
Step 4: Calculate the potential difference (V') across the 50 cm segment
Using Ohm's law again, the potential difference (V') can be calculated as:
V′=I⋅R′
Substituting the values:
V′=0.06A⋅(503Ω)
Calculating:
V′=0.06⋅16.67≈1V
Conclusion
The potential difference between the two points on the wire separated by a distance of 50 cm is approximately 1 V.
---
- Voltage of the battery (V) = 6 V
- Length of the wire (L) = 3 m
- Resistance of the wire (R) = 100 Ω
- Distance between the two points on the wire (L') = 50 cm = 0.5 m
Using Ohm's law, the current (I) can be calculated using the formula:
I=VR
Substituting the values:
I=6V100Ω=0.06A
To find the resistance of the 50 cm segment of the wire, we can use the formula for resistance:
R′=R⋅L′L
Where:
- R is the total resistance of the wire,
- L′ is the length of the segment we are interested in (0.5 m),
- L is the total length of the wire (3 m).
R′=100Ω⋅0.5m3m=503Ω≈16.67Ω
Using Ohm's law again, the potential difference (V') can be calculated as:
V′=I⋅R′
Substituting the values:
V′=0.06A⋅(503Ω)
Calculating:
V′=0.06⋅16.67≈1V
The potential difference between the two points on the wire separated by a distance of 50 cm is approximately 1 V.
Similar Questions
A battery of 6 volts is connected ot the termainals of a three meter long wire of uniform thickness and resistance of the order of 100Ω. The difference of potential between two points separated by 50cm on the wire will
View SolutionA potentiometer consists of a wire of length 4 m and resistance 10Ω. It is connected to a cell of emf 2V.The potential gradient of the wire is
View Solution
Knowledge Check
A voltmeter having a resistance of 1800Ω employed to measure the potential difference across a 200Ω resistor which is connected to the terminals of a dc power supply having an emf of 50 V and an internal resistance of 20Ω. What is the percentage decrease in the potential difference across the 200Ω resistor as a result of connecting the voltmeter across it?
A1%B5%C10%D25%
If a ideal battery of e.m.f.10 V is connected with external resistance 9Ω and a wire of length 10 m and resistance 1Ω in series as shown. Then the potential gradient of wire is

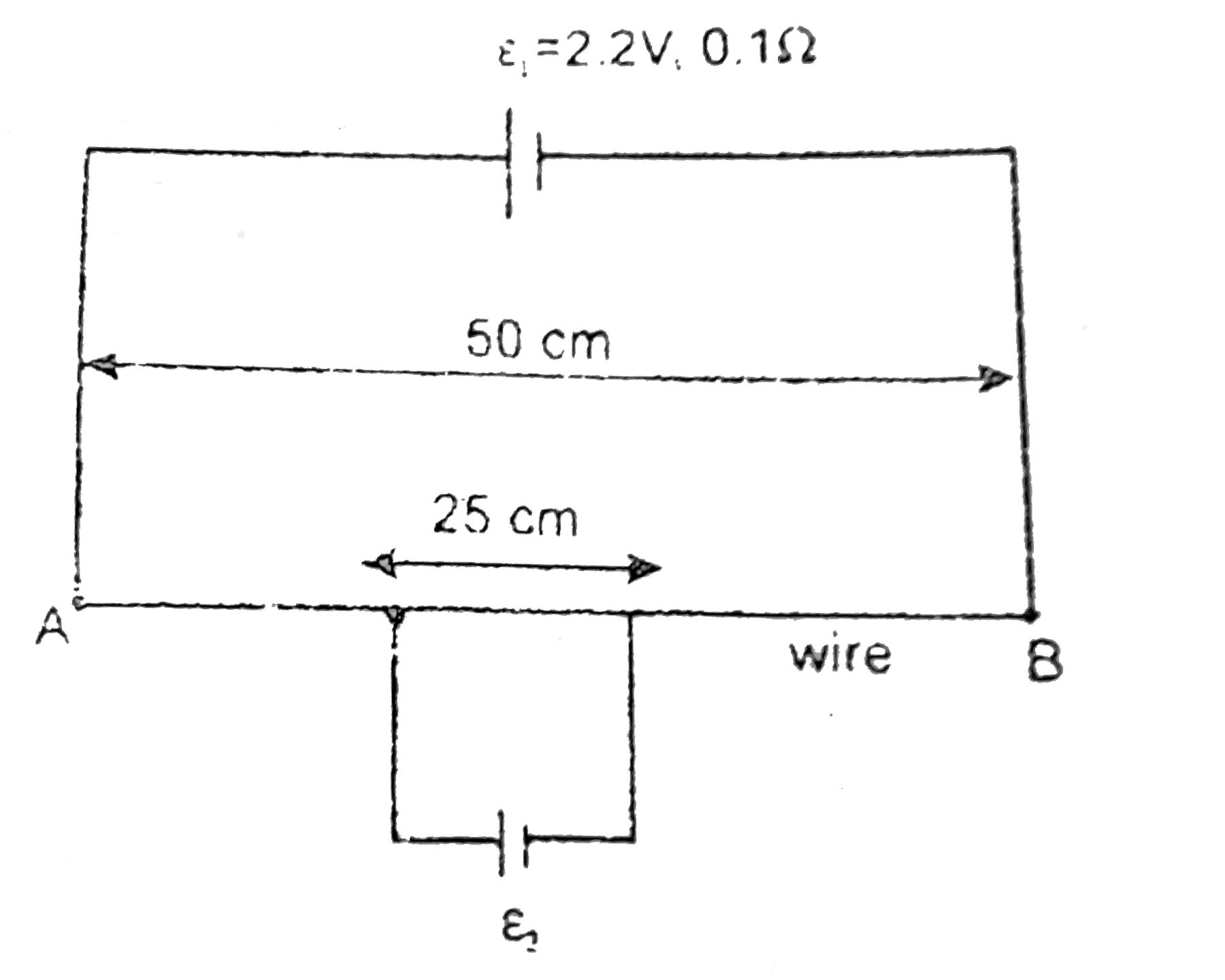
View SolutionA thin uniform wire AB of length 50 cm and resistance 1Ω is connected to be terminals of a battery of emf ε1=2.2V and internal resistance 0.1Ω. If the terminals of another cell (assume ideal) are connected to two points 25 cm apart on the wire AB without altering the current in the wire AB, the emf ε2 of cell in volts is :
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View SolutionIn a potentiometer, a uniform potential gradient of 0.8Vm−1 is maintained across its 10 m wire . The potential difference across two points on the wire located at 65 cm and 2.45 m is
View SolutionA uniform wire of resistance (50Ω)is cut into 5 equal parts. These parts are now connected in parallel.the Equivalent resistance of the combination is
View Solution

