A circular disc is to be made using iron and aluminium. To keep its moment of inertia maximum about a geometrical axis, it should be so prepared that
Aluminium at interior and iron surround to it
Iron at interior and aluminium surround to it
Using iron and aluminium layers in alternate order
Sheet of iron is used at both external surface and aluminium sheet as internal layers
The correct Answer is:A
Density of iron is more than Aluminium
Similar Questions
A circular disc is to be made by using iron and aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It is possible with
View SolutionThe rotational inertia of a disc about its geometrical axis does not depend upon its
View SolutionA solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
View SolutionA circular disc of radius R and thickness R6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
View SolutionA thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be :
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View SolutionA circular disc of radius R and thickness R6 has moment of inertia about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
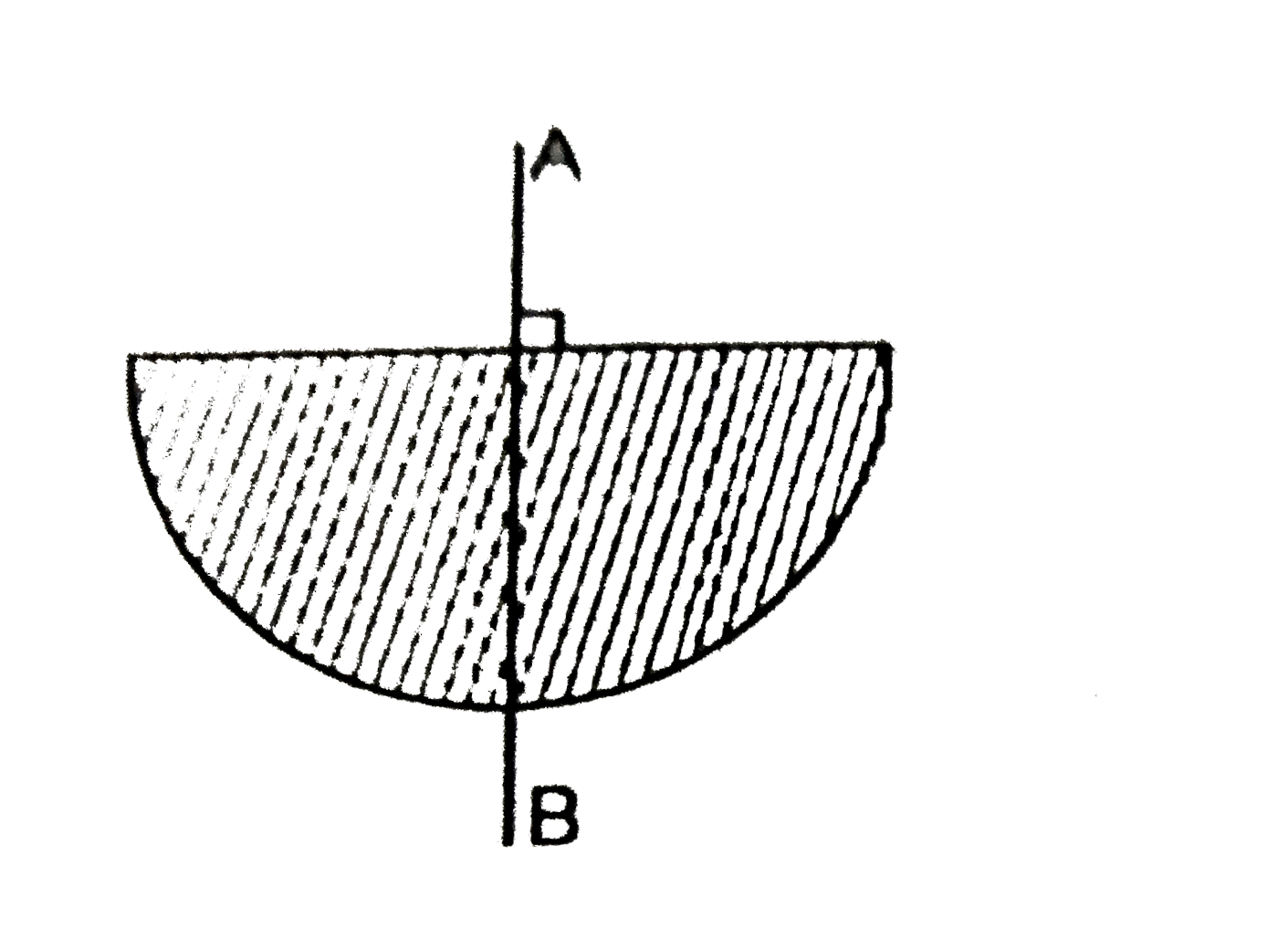
View Solution
