In a regular octahedral molecule MX6 the number of X−M−X bonds at 180∘ is
3
2
6
4
The correct Answer is:A
To solve the problem of determining the number of X−M−X bonds at 180° in a regular octahedral molecule MX₆, we can follow these steps:
1. Understand the Structure of Octahedral Molecule:
- An octahedral molecule has a central atom (M) surrounded by six atoms (X) at the corners of an octahedron. The geometry is symmetrical.
2. Visualize the Octahedral Geometry:
- In an octahedral arrangement, the six X atoms are positioned such that four of them lie in the same plane (forming a square), while the other two are positioned above and below this plane.
3. Identify the Bond Angles:
- In this structure, the angles between the bonds are crucial. The bonds in the plane are at 90° to each other, while the bonds that extend above and below the plane are 180° apart from each other.
4. Count the 180° Bonds:
- To find the number of X−M−X bonds that are at 180°, we can analyze the pairs:
- The two X atoms in the same plane can be paired with the two X atoms in the opposite plane (above and below), which gives us one pair.
- Additionally, the two X atoms in the plane can be paired with each other, which gives us another pair.
- Finally, the bond extending above the plane and the bond extending below the plane also forms a 180° angle.
5. Total Count:
- Therefore, we have three distinct pairs of X−M−X bonds that are at 180°.
Final Answer:
The number of X−M−X bonds at 180° in a regular octahedral molecule MX₆ is 3.
---
- An octahedral molecule has a central atom (M) surrounded by six atoms (X) at the corners of an octahedron. The geometry is symmetrical.
- In an octahedral arrangement, the six X atoms are positioned such that four of them lie in the same plane (forming a square), while the other two are positioned above and below this plane.
- In this structure, the angles between the bonds are crucial. The bonds in the plane are at 90° to each other, while the bonds that extend above and below the plane are 180° apart from each other.
- To find the number of X−M−X bonds that are at 180°, we can analyze the pairs:
- The two X atoms in the same plane can be paired with the two X atoms in the opposite plane (above and below), which gives us one pair.
- Additionally, the two X atoms in the plane can be paired with each other, which gives us another pair.
- Finally, the bond extending above the plane and the bond extending below the plane also forms a 180° angle.
- Therefore, we have three distinct pairs of X−M−X bonds that are at 180°.
The number of X−M−X bonds at 180° in a regular octahedral molecule MX₆ is 3.
Similar Questions
In a regular octahedral molecule SF6 the number of F−S−F bonds at 180∘ is .
View SolutionIn a regular trigonal bipyramidal MX5, the number of X - M - X bonds at 180∘ is
View SolutionA sigma bonded molecule MX3 is T-shaped The number of non-bonding pairs of electrons is .
View SolutionThe number of C-H bonds in ethane molecule are :
View SolutionIf a molecule MX3 has zero dipole moment, the state hybridisation of M is :
View SolutionWrite the correct form of the following statement:
In a methane molecule, the number of C-H bonds is 6.
View SolutionNumber of H−bonds formed by a water molecule is:
View SolutionWrite the number of σ and π bonds in the following molecules?
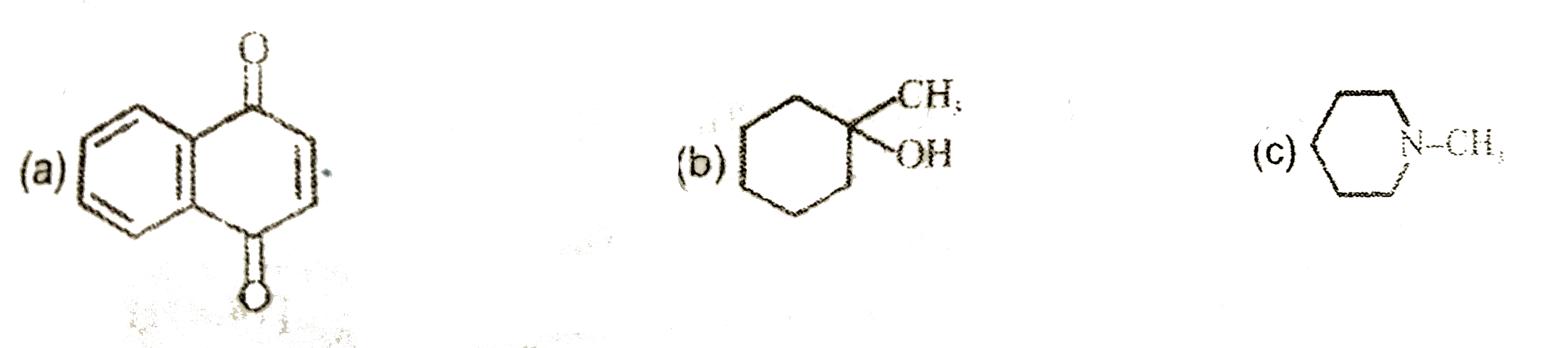
View SolutionA mineral MX2 crystallizes in ccp of M2+ ions whereas X− ions occupy the tetrahedral voids. The number of cations and anions per unit cell, the coordination number of cation and percent of tetrahedral voids occupied are :
View SolutionConsider Al2(OH)6 compound and calculate the vale of (X+Y):=Z
Where X= Total number of (2c−2e−) bond.
Where Y=Total number of (3c−2e−) bond.
Where Z= Total number of (3c−4d−) bond.
View Solution
