Which one is the wrong statement ?
de-Broglie's wavelength is given by λ=hmv,
where
m = mass of the particle,
v = group velocity of the particle
The uncertainty principle is ΔE×Δt≥h/4π
Half-filled and fully filled orbitals have greater stability due to greater exchange energy, greater symmetry and more balanced arrangement
The energy of 2s-orbital is less than the energy of 2 p-orbital in case of hydrogen like atoms
The correct Answer is:D
To determine which statement is incorrect, let's analyze each statement one by one based on the principles of atomic structure and quantum mechanics.
Step 1: Analyze Statement A
Statement A: "De Broglie wavelength is given by h/mv."
- The de Broglie wavelength (λ) is indeed given by the formula:
λ=hp
where p is the momentum of the particle. Since momentum p is defined as mv (mass times velocity), we can rewrite the equation as:
λ=hmv
Thus, Statement A is correct.
Step 2: Analyze Statement B
Statement B: "Heisenberg's uncertainty principle states that the uncertainty in position and uncertainty in momentum is greater than or equal to h/4π."
- Heisenberg's uncertainty principle is mathematically expressed as:
Δx⋅Δp≥h4π
where Δx is the uncertainty in position and Δp is the uncertainty in momentum. Therefore, Statement B is also correct.
Step 3: Analyze Statement C
Statement C: "Half filled and fully filled orbitals have greater stability due to greater exchange energy, greater symmetry, and more balanced arrangement."
- This statement is true because half-filled and fully filled orbitals do exhibit greater stability due to exchange energy and symmetry. Therefore, Statement C is correct.
Step 4: Analyze Statement D
Statement D: "The energy of the 2s orbital is less than the energy of the 2p orbital."
- In hydrogen-like atoms, the energy levels depend only on the principal quantum number n and not on the azimuthal quantum number l. For hydrogen-like atoms, the energy of the 2s and 2p orbitals is the same:
En=−13.6eV⋅Z2n2
Therefore, Statement D is incorrect because it implies that the 2s orbital has lower energy than the 2p orbital, which is not true for hydrogen-like atoms.
Conclusion
The wrong statement among the given options is Statement D.
---
Statement A: "De Broglie wavelength is given by h/mv."
λ=hp
where p is the momentum of the particle. Since momentum p is defined as mv (mass times velocity), we can rewrite the equation as:
λ=hmv
Thus, Statement A is correct.
Statement B: "Heisenberg's uncertainty principle states that the uncertainty in position and uncertainty in momentum is greater than or equal to h/4π."
Δx⋅Δp≥h4π
where Δx is the uncertainty in position and Δp is the uncertainty in momentum. Therefore, Statement B is also correct.
Statement C: "Half filled and fully filled orbitals have greater stability due to greater exchange energy, greater symmetry, and more balanced arrangement."
Statement D: "The energy of the 2s orbital is less than the energy of the 2p orbital."
En=−13.6eV⋅Z2n2
Therefore, Statement D is incorrect because it implies that the 2s orbital has lower energy than the 2p orbital, which is not true for hydrogen-like atoms.
The wrong statement among the given options is Statement D.
Similar Questions
Knowledge Check
Which one is wrong statement?
ATotal orbital angular momentum of electron in 's' orbital is equal to zeroBAn orbital is designated by three quantum numbers while an electron in an atom is designated by four quntum numbersCThe electronic configuration of N atoms is DThe value of m for d2Z is zero
DThe value of m for d2Z is zero
Which one is a wrong statement?
View SolutionThree arrangements are shown for the complexes [CoBr2(NH3)2(en)]⊕. Which one is wrong statement?
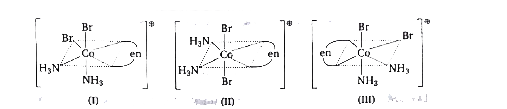
View SolutionWhich is the wrong statement ?
View SolutionAmong the following which one is a wrong statement-
View SolutionWhich one is wrong statement
View SolutionWhich one of the given statements is wrong?
View SolutionWhich of the following is the wrong statement ?
View Solution
