The focal lengths of a converging lens measured for violet, green and red colours of respectively. We will find
(A).
(B).
(C).
(D).
The correct Answer is:B
Step by step video & image solution for The focal lengths of a converging lens measured for violet, green and red colours of fv'f_(G)'f_(R) respectively. We will find (A). f_(R)gtf_(G)gtf_(V) (B). f_(v)ltf_(R)ltf_(G) (C). f_(V)gtf_(R)gtf_(G) (D). f_(V)=f_(R)=f_(G) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Knowledge Check
- Question 1 - Select One
When f:R→Randg:R→R are two functions defined by f(x)=8x3andg(x)==x13 respectively and (g of ) (x) = k (f o g ) (x) , then k is
A4B2C12DNone of these
Similar Questions
The focal length ofa converging lens are fvandfr for violet and red light respectively.
View SolutionThe focal length of a converting lens are fvandfr for violet and red lights, respectively. Which of the following is correct?
View SolutionIf f(V) and fR are the focal lengths of a convex lens for violet and red light respectively and FVand FR are the focal lengths of concave lens for violet and red light respectively, then we have
View SolutionIf f,g:R→R be defined by f(x)=2x+1 and g(x)=x2−2,∀x∈R, respectively. Then , find gof .
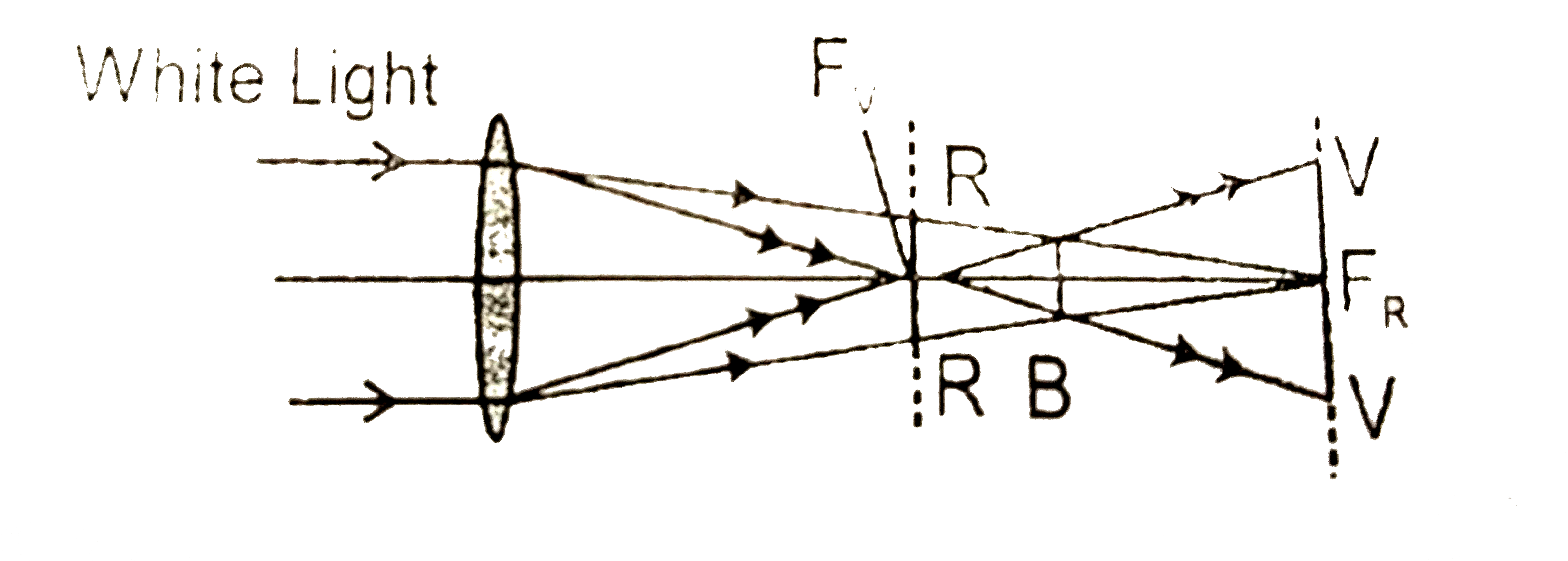
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)

Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration of a lens can be corrected by :View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
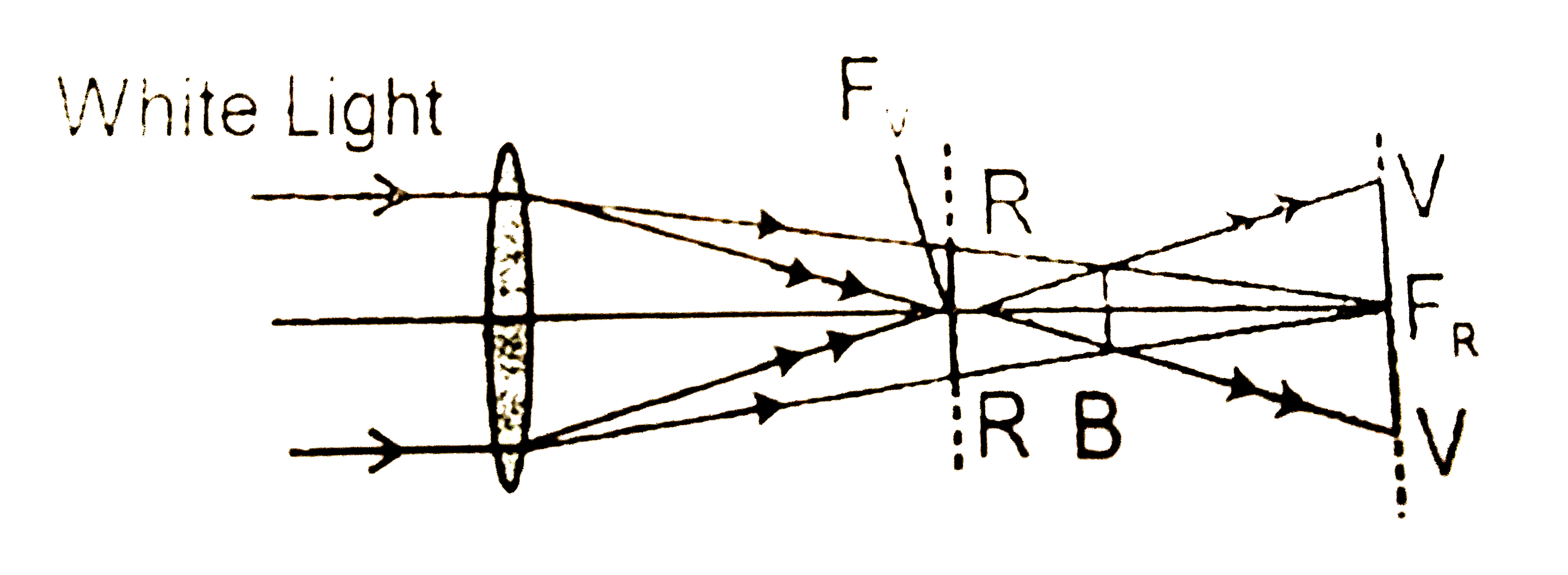
The dispersive power of crown and fint glasses are 0.02 and 0.04 respectively. An achromtic converging lens of focal length 40cm is made by keeping two lenses, one of crown glass and the other of flint glass, in contact with each other. The focal lengths of the two lenses are :View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)

Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration in the formation of image by a lens arises because :View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
A combination is made of two lenses of focal lengths f and f' in contact , the dispersive powers of the materials of the lenses are ω and ω' . The combination is achromatic when :View SolutionIf f,g, h are three functions defined from R → R as follows: Find the range of f(x)=x2
View Solution

