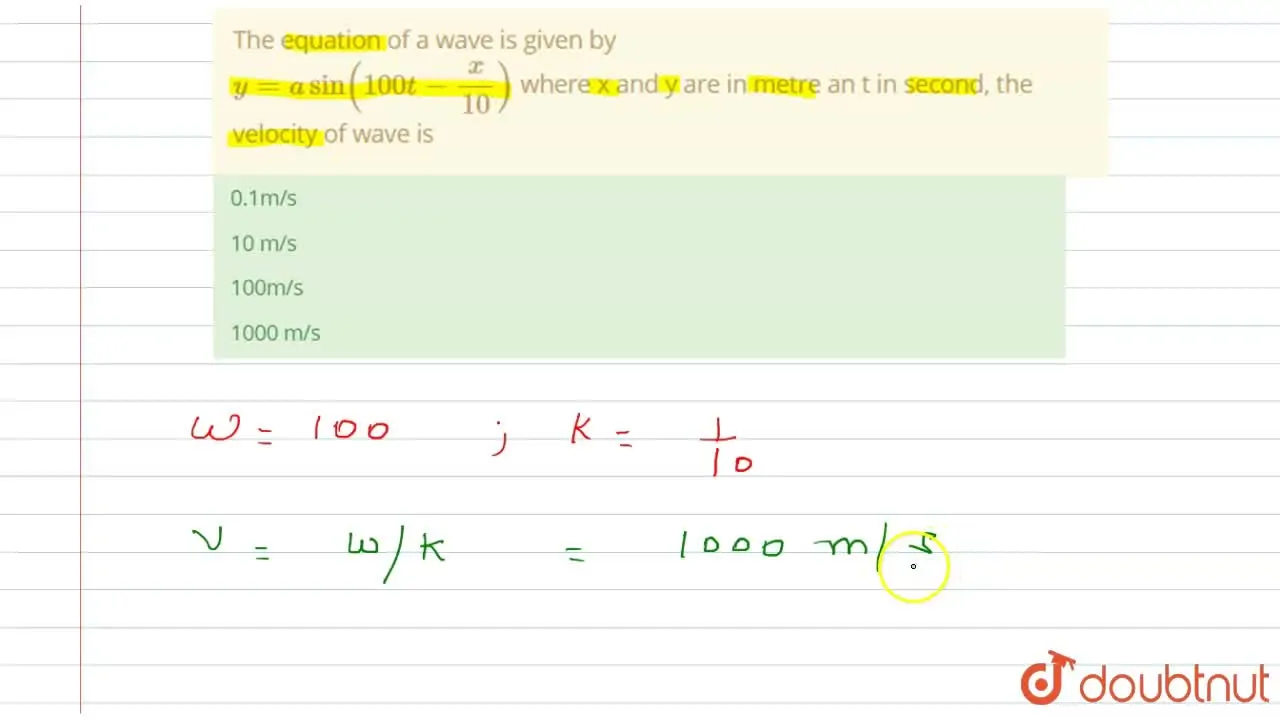
The equation of a wave is given by
y=asin(100t−x10) where x and y are in metre an t in second, the velocity of wave is
0.1m/s
10 m/s
100m/s
1000 m/s
The correct Answer is:d
Step by step video & image solution for The equation of a wave is given by y=a sin (100t-x/10) where x and y are in metre an t in second, the velocity of wave is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The equation of progressive wave is given by y=10sin[300π(t−x480)]
where x and y are in metre and t is in second. Calculate the amplitude frequency time period and wavelength of the wave.View SolutionThe equation of a wave id represented as Y=2sin(Πx−200Πt) where x and y are in cm and t is in second. The wave velocity is
View SolutionThe equation of a simple harmonic wave is given by Y=5sinπ2(100t−x), where x and y are in metre and time is in second. The time period of the wave (m seconds) will be
View SolutionThe equation of a plane progressive wave is given by
y=2cos(100πt−πx20)
where x and y are in cm and t is in second. The wavelength of the wave isView SolutionThe equation of a plane progressive wave is given by
y=2sin(100πt−πx20)
where x and y are in cm and t is in second. The amplitude and the initial phase of the wave are respectively.View SolutionA travelling wave pulse is given by
y=43x2+48t2+24xt+2
where x and y are in metre and t is in second. The velocity of wave is :-View SolutionThe equation of a transverse wave is given by
y=10sinπ(0.01x−2t)
where x and y are in cm and t is in second. Its frequency isView SolutionThe equation of wave is given as y=7sinΠ(x−50t) where x and y are in cm t is in s. The ratio of wave velocity and maximum particle velocity is
View SolutionThe equation of a transverse wave is given by y=10sin2Π(2x−3t) where x and y are in cm and t is in s. Its frequency is
View SolutionThe equation of a simple harmonic wave is given by
y=3sinπ2(50t−x)
where x and y are in meters and x is in second .The ratio of maximum particle velocity to the wave velocity isView Solution