A mass m is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break when:
inclined at a angle of 60∘ from vertical
the mass is at the highest point
the wire is horizontal
the mass is at the lowest point
The correct Answer is:D
To solve the problem of determining when the wire is most likely to break while a mass m is whirled in a vertical circle, we need to analyze the tension in the wire at different positions of the mass. The wire is most likely to break when the tension is at its maximum.
1. Identify the Positions: The mass can be at four different positions in the vertical circle:
- A: At an angle of 60 degrees from the vertical.
- B: At the highest point of the circle.
- C: At the horizontal position.
- D: At the lowest point of the circle.
2. Analyze Tension at Each Position:
- Position A (60 degrees from vertical):
- The forces acting on the mass are its weight mg acting downward and the tension T in the wire acting inward.
- The centripetal force required for circular motion is provided by the net force towards the center:
T+mgcos(60∘)=mv2R
- Since cos(60∘)=12:
T+mg2=mv2R
T=mv2R−mg2
- Position B (Highest Point):
- At the highest point, both the weight and tension act downward:
T+mg=mv2R
T=mv2R−mg
- Position C (Horizontal Position):
- At this position, the weight acts downward and tension acts horizontally:
T=mv2R
- Position D (Lowest Point):
- At the lowest point, the weight acts downward and tension acts upward:
T−mg=mv2R
T=mg+mv2R
3. Compare Tensions:
- From the equations derived:
- Position A: T=mv2R−mg2
- Position B: T=mv2R−mg
- Position C: T=mv2R
- Position D: T=mg+mv2R
4. Determine Maximum Tension:
- Among all positions, the tension is maximum at Position D (Lowest Point):
T=mg+mv2R
- This indicates that the wire is most likely to break when the mass is at the lowest point of the vertical circle.
Conclusion:
The wire is most likely to break when the mass is at the lowest point of the vertical circle. Therefore, the correct answer is Option D.
- A: At an angle of 60 degrees from the vertical.
- B: At the highest point of the circle.
- C: At the horizontal position.
- D: At the lowest point of the circle.
- Position A (60 degrees from vertical):
- The forces acting on the mass are its weight mg acting downward and the tension T in the wire acting inward.
- The centripetal force required for circular motion is provided by the net force towards the center:
T+mgcos(60∘)=mv2R
- Since cos(60∘)=12:
T+mg2=mv2R
T=mv2R−mg2
- At the highest point, both the weight and tension act downward:
T+mg=mv2R
T=mv2R−mg
- At this position, the weight acts downward and tension acts horizontally:
T=mv2R
- At the lowest point, the weight acts downward and tension acts upward:
T−mg=mv2R
T=mg+mv2R
- From the equations derived:
- Position A: T=mv2R−mg2
- Position B: T=mv2R−mg
- Position C: T=mv2R
- Position D: T=mg+mv2R
- Among all positions, the tension is maximum at Position D (Lowest Point):
T=mg+mv2R
- This indicates that the wire is most likely to break when the mass is at the lowest point of the vertical circle.
The wire is most likely to break when the mass is at the lowest point of the vertical circle. Therefore, the correct answer is Option D.
Similar Questions
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
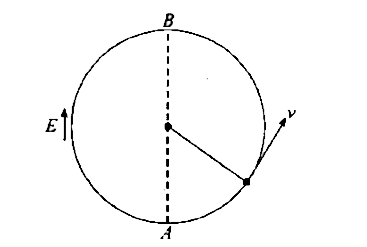
View Solution
Knowledge Check
The diameter of a thin wire can be measured by :
Aa vernier callipersBa metre ruleCa screw gaugeDnone of these.A 1 kg stone at the end of 1 m long string is whirled in a vertical circle at constant speed of 4 m/sec. The tension in the string is 6 N when the stone is at (g=10m/sec2)
Atop of the cirlceBbottom of the circleChalf way downDnone of the above
A stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
View SolutionA stone of mass 1kg is tied with a string and it is whirled in a vertical circle of radius 1 m. If tension at the highest point is 14 N, then velocity at lowest point will be
View SolutionA mass of 20kg is attached to one end of a steel wire 50cm long and is rotated in a horizontal circle. The area of cross-section of the wrie is 10−6m2 and the breaking stress for it is 4.8×107Pa. Calculate the maximum velocity with which the mass can be rotated.
View SolutionAn object of mass 10kg is attached to roof by string whirled round a horizontal circle of radius 4 and 30∘ to the vertical. The tension in the string (approximately) is
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View Solution

